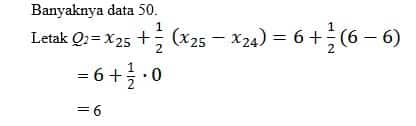Matematika sendiri memiliki beberapa cabang pembelajaran, seperti statistik, bilangan, rumus-rumus bangun ruang, serta penggunaan sinus, cosinus, dan sebagainya. Dalam hal ini kami membahas statistik, dimana statistik berguna guna mengumpulkan data untuk membuat atau menarik suatu keputusan, untuk membandingkan sesuatu dan lain-lain. Pada umumnya, statistik disajikan dalam bentuk tabel atau diagram agar udah dibaca, dipahami, dan dianalisis.
Baca Juga Artikel Yang Mungkin Berhubungan : Rumus Kerucut : Volume Luas Permukaan, Tinggi, Dan Gambar
Pengertian Kuartil
Kuartil adalah nilai atau angka yang membagi data dalam empat bagian yang sama, setelah disusun dari data yang terkecil sampai data terbesar atau sebaliknya dari data terbesar sampai data terkecil.
Ada tiga bentuk data kuartil, yaitu :
- Kuartil Pertama ialah nilai dalam distribusi yang membatasi 25% frekuensi di bagian atas dan 75% di bagian bawah distribusi.
- Kuartil Kedua ialah nilai dalam distribusi yang membatasi 50% frekuensi di bagian atas dan 50% di bagian bawah distribusi.
- Kuartil Ketiga ialah nilai dalam distribusi yang membatasi 75% frekuensi di bagian atas dan 25% di bagian bawah distribusi.
Pengertian Kuartil Menurut Para Ahli
- Menurut Sudijono, 2006:112. Dalam dunia statistik, yang dimaksud dengan kuartil adalah titik atau skor atau nilai yang membagi seluruh distribusi frekuensi kedalam empat bagian yang sama besar, yaitu masing-masing sebesar 1/4N. Jadi di sini akan kita jumpai tiga buah kuartil, yaitu kuartil pertama (K1), Kuartil kedua (K2), dan Kuartil ketiga (K3). Ketiga Kuartil inilah yang membagi seluruh distribusi frekuensi dari data yang kita selidiki menjadi empat bagian yang sama besar, masing-masing sebesar 1/4N.
- Wirawan,2001:105. Kuartil (K) adalah nilai-nilai yang membagi serangkaian data atau suatu distribusi frekuensi menjadi empat (4) bagian yang sama. Ada tiga Kuartil yaitu kuartil pertama (K1), kuartil kedua (K2), dan kuartil ketiga (K3).
- Pendapat Sudjana,2005:81. Jika sekumpulan data dibagi menjadi empat bagian yang sama banyak, sesudah disusun menurut urutan nilainya, maka bilangan pembaginya disebut kuartil. Ada tiga buah kuartil, ialah kuartil pertama, kuartil kedua dan kuartil ketiga yang masing-masing disingkat dengan K1, K2, K3. Pemberian nama ini dimulai dari nilai kuartil paling kecil.
Baca Juga Artikel Yang Mungkin Berhubungan : Rumus Volume Tabung : Luas Permukaan, Luas Selimut, Tinggi, & Contoh Soal
Jika sekelompok data dibagi menjadi dua bagian yang sama, maka nilai yang berada di tengah (50%) disebut dengan median. Konsep median dapat diperluas yaitu kelompok data yang telah diurutkan (membesar atau mengecil) dibagi menjadi empat bagian sama banyak. Bilangan pembagi ada tiga masing masing disebut Kuartil yaitu Kuartil Pertama / Bawah (Q1), Kuartil Kedua / Tengah (Q2) dan Kuartil Ketiga / Atas (Q3).
Jika sekumpulan data dibagi menjadi empat bagian yang sama banyaknya dan sudah disusun menurut urutan nilainya, maka bilangan pembaginya disebut Kuartil, ada tiga buah Kuartil ialah Kuartil Pertama, Kurtil Kedua Dan Kuartil Ketiga yang masing masing disingkat menjadi Q1, Q2 dan Q3 pemberian nama ini dimulai dari Kuartil yang paling kecil.
Untuk menentukan nilai Kuartil dengan langkah berikut :
-
KUARTIL DATA TIDAK BERKELOMPOK
- Data disusun menurut urutan nilainya
- Menentukan letak kuartil dengan rumus
Rumus Kuartil
Qi = Nilai yang ke – i (n+1) dimana i = 1,2,3
4
-
KUARTIL DATA BERKELOMPOK
( (in / 4) – F
Qi = Lo + C x ( —————— ) dimana i = 1,2,3
f
dimana :
Lo = Batas Bawah Kelas Kuartil
C = lebar Kelas
F = jumlah Frekuensi semua kelas sebelum kelas Kuartil Qi
f = Frekuensi Kelas Kuartil Qi
Baca Juga Artikel Yang Mungkin Berhubungan : 54 Gambar Jaring jaring Balok, Rumus, Dan Cara Membuat
Contoh Cara perhitungan kuartil untuk data tunggal
Misalkan dari 60 orang siswa MAN Jurusan IPA diperoleh nilai hasil EBTA bidang studi Fisika sebagaimana tertera pada table distribusi frekuensi berikut ini. Jika kita ingin mencari Q1, Q2, dan Q3 (artinya data tersebut akan kita bagi dalam empat bagian yang sama besar), maka proses perhitungannya adalah sebagai berikut:
Table 3.11. Distribusi frekuensi nilai hasil Ebta dalam bidang studi fisika dari 60 orang siswa MAN jurusan ipa, dan perhitungan Q1, Q2, dan Q3.
| Nilai (x) | F | Fkb |
| 46
45 44 43 42 41 40 39 38 37 36 35 |
2
2 3 5 F1 (8) 10 F1 (12) F1 (6) 5 4 2 1 |
60= N
58 56 53 48 40 30 18 12 7 3 1 |
Jawaban
Titik Q1= 1/4N = ¼ X 60 = 15 ( terletak pada skor 39). Dengan demikian dapat kita ketahui: 1=
38,50; fi = 6; fkb = 12
Q1 = 1 + ( n/4N-fkb) = 38,50 +(15-12)
Fi 6
= 38,50 +0,50
= 39
Titik Q2= 2/4N = 2/4 X 60 = 30 ( terletak pada skor 40). DenganØ demikian dapat kita ketahui: 1=
39,50; fi = 12; fkb = 18
Q2 = 1 + ( n/4N-fkb) = 39,50 +(30-18)
Fi 12
= 39,50 +1,0
= 40,50
Titik Q3= 3/4N = 3/4 X 60 = 45 ( terletak pada skor 42). Dengan demikian dapat kita ketahui: 1= 41,50; fi = 8; fkb = 40Ø
Q3 = 1 + ( n/4N-fkb) = 41,50 +(45-40)
Fi 8
= 41,50+ 0,625
= 42,125
Baca Juga Artikel Yang Mungkin Berhubungan : Jaring Jaring Kubus : 11 Gambar Pola Dan Cara Membuat
Contoh Cara perhitungan kuartil untuk data kelompok
Misalkan dari 80 orang siswa MAN jurusan IPS diperoleh skor hasil EBTA dalam bidan studi tata buku sebagaimana disajikan pada tabel distribusi frekuensi beikut ini ( lihat kolom 1 dan 2). Jika kita ingin mencari Q1, Q2, dan Q3, maka proses perhitungannya adalah sebagai berikut:
Titik Q1= 1/4N = ¼ X 80 = 20 ( terletak pada interval 35-39). DenganØ demikian dapat kita ketahui: 1= 34,50; fi = 7; fkb = 13, i= 5.
Q1 = 1 + ( n/4N-fkb) Xi = 34,50 +(20-13) X5
Fi 7
= 34,50 +5
= 39,50
Titik Q2= 2/4N = 2/4 X 80 = 40 ( terletak pada interval 45-49).Ø Dengan demikian dapat kita ketahui: 1= 44,50; fi = 17; fkb = 35, i= 5.
Q1 = 1 + ( n/4N-fkb) Xi = 44,50 +(40-35) X5
Fi 17
= 44,50 +1.47
= 45,97
Titik Q3= 3/4N = 3/4 X 80 = 60 ( terletak pada interval 55-59).Ø Dengan demikian dapat kita ketahui: 1= 54,50; fi = 7; fkb = 59, i= 5.
Q1 = 1 + ( n/4N-fkb) Xi = 54,50 +(55-59) X5
Fi 7
= 54,50 + 0,71
= 55,21
Tabel 3.12. distribusi frekuensi skor-skor hasil EBTA bidang studi tata buku dari 80 orang siswa man jurusan ips, berikut perhitungan Q1,Q2, dan Q3.
| Nilai (x) | F | Fkb |
| 70-74
65-69 60-64 55-59 50-54 45-49 40-44 35-39 30-34 25-29 20-24 |
3
5 6 7 7 17 15 7 6 5 2 |
80
77 72 66 59 52 35 20 13 7 2 |
| Total | 80= N | – |
Diantara kegunaan kuartil adalah untuk mengetahui simetris (normal) atau a simetrisnya suatu kurva. Dalam hal ini patokan yang kita gunakan adalah sebagai berikut:
- 1). Jika Q3-Q2 = Q2- Q1 maka kurvanya adalah kurva normal.
- 2). Jika Q3-Q2 > Q2- Q1 maka kurvanya adalah kurva miring/ berat ke kiri(juling positif).
- 3). Jika Q3-Q2 < Q2- Q1 maka kurvanya adalah kurva miring/ berat ke kanan(juling negatif).
Jika data disajikan dalam bentuk Data Tunggal Tak Berfrekuensi
Rumus: Qi = 1 x ((n + 1) : 4) atau 2 x ((n + 1) : 4) atau 3 x ((n + 1) : 4)
Contoh:
Tentukan kuartil dari data berikut: 71, 69, 70, 48, 79, 61, 69, 83, 57, 54, 90,
ð 48, 54, 57, 61, 69, 69, 70, 71, 79, 83, 90
Kuartil 1 = 57
Kuartil 2 = 79
Data Tunggal Berfrekuensi
Contoh 2 :
Tentukandari tabel berikut :
Tabel 1
| Nilai | f |
| 4 | 1 |
| 5 | 2 |
| 6 | 4 |
| 7 | 3 |
| 8 | 2 |
Jawab : Tentukan terlebih dahulu frekuensi kumulatif sebagai berikut
Tabel 2
| Nilai | f | ∑f |
| 4 | 1 | 1 |
| 5 | 2 | 1+2=3 |
| 6 | 4 | 3+4=7 |
| 7 | 3 | 7+3=10 |
| 8 | 2 | 10+2=12 |
Jadi jumlah frekuensi (atau jumlah data) ada n=12,
Q2 ditentukan dahulu karena menentukan yang tengah-tengah paling mudah, dan tengah-tengah dari 12 data terletak antara data ke-6 dan ke-7 seperti nampak pada visualisasi berikut :
Dengan melihat tabel 2, kita tahu bahwa data ke-6 adalah 6 dan data ke-7 juga 6, sehingga Q2= (6+6)/2 = 6
Secara umum, mencari nilai Q1, Q2, dan Q3 adalah dengan cara memandang jumlah data secara kontinu atau dipandang seperti sebuah garis lurus, misalnya sebagai berikut untuk contoh diatas :
Data Berkelompok
Contoh 2 :
| Interval | f | ∑f |
| 5 – 8 | 2 | 2 |
| 9 – 12 | 4 | 6 |
| 13 – 16 | 5 | 11 |
| 17 – 20 | 3 | 14 |
Dari tabel di atas, kita peroleh :
Banyak interval ada 4, yaitu 5 – 8, 9 – 12, 13 – 16, 17 – 20 ;
Panjang masing-masing kelas (interval), c = (8 – 5) + 1 = 4 ;
Banyak data, n=∑f=14 ;
Tepi bawah masing-masing interval didefinisikan dengan batas bawah dikurangi 0,5, dan tepi atas didefinisikan dengan batas atas ditambah 0,5. Tepi bawah masing-masing interval adalah : 4,5 ; 8,5 ; 12,5 ; 16,5 . Tepi atas masing-masing interval adalah : 8,5 ; 12,5 ; 16,5 ; 20,5.
Karena median (Q2) terletak di tengah-tengah, maka merupakan data ke-n/2=data ke-14/2=7. Dengan melihat tabel, data ke-7 terletak pada interval ketiga, yang tepi bawahnya, B=12,5.
Kuartil kedua (Q2) dinyatakan dengan formulasi :
dengan fk adalah frekuensi kumulatif sebelum kelas yang memuat Q2 (dalam contoh ini kelas median adalah kelas ketiga), jadi fk = 6 ;dan f adalah frekuensi kelas median, yaitu f = 5.Sehingga dapat kita hitung
Contoh lain kuartil :
Misal, untuk menentukan kuartil dari kumpulan data berikut.
- Data ganjil:
13 8 11 25 18 1 9. Tentukan K1-nya
Jawab:
Urutan datanya:
1 8 9 11 13 18 25
Letak kuartil (Q1 = ada pada data yang kedua atau Q1 = 8
- Data genap
8 12 5 3 7 2 3 9.
Urutan data:
2 3 3 5 7 8 9 12
Q1= misal menentukan nilai Q2 maka: Letak Q2 = (terletak pada data yang keempat koma lima). Setelah kita dapatkan letak dari Q2, selanjutnya menentukan nilai K2 sebagai berikut:
Nilai Q2 = data keempat + (data kelima – data keempat)
Q2 = 5 + (7-5) = 7
Contoh 2:
Diketahui data sebagai berikut : 7, 6, 4, 5, 6, 5, 7, 6, 8, 4, 7, 8.
Tentukan Q1, Q2, dan Q3 !
Jawab:
Setelah diurutkan : 4, 4, 5, 5, 6, 6, 6, 7, 7, 7, 8, 8 dan n = 12
Baca Juga Artikel Yang Mungkin Berhubungan : Flowchart Adalah : Simbol Flowchart, Contoh, Dan Cara Membuatnya
Pengertian Desil
Desil atau disingkat dengan (Ds) adalah nilai atau angka yang membagi data yang menjadi 10 bagian yang sama, setelah disusun dari data terkecil sampai data terbesar atau sebaliknya. Cara mencari desil hampir sama dengan mencari nilai kuartil, bedanya hanya pada pembagian saja. Kalau kuartil data dibagi empat bagian yang sama, sedangkan desil data dibagi 10 bagian yang sama. Harga-harga desil ada sembilan bagian, yaitu Ds1 sampai Ds9.
Sedangkan Desil Menurut Para Ahli Adalah
- Desil (D) adalah titik atau skor atau nilai yang membagi seluruh distribusi frekuensi dari data yang diselidiki ke dalam 10 bagain yang sama besar, yang masing-masing sebesar 1/10 N (Sudijono, 2006: 117-118). Jadi, sebanyak 9 buah titik desil, keseimbilan buah desil itu membagi seluruh distribusi frekuensi ke dalam 10 bagian yang sama besar.
- Desil adalah nilai-nilai yang membagi seangkaian data atau suatu distribusi frekuensi menjadi sepuluh bagian yang sama (Wirawan, 2001: 110). Jadi ada sembilan ukuran desil.
- Jika sekumpulan data itu dibagi menjadi 10 bagian yang sama, maka didapat sembilan pembagi dan setiap bagiam dinamakan desil (Sudjana, 2005: 82). Karenanya ada sembilan buah desil, ialah desil pertama, desil kedua, desil, ketiga, desil keempat, desil kelima, desil keenam, desil ketujuh, desil kedelapan, dan desil kesembilan yang disingkat dengan D1, D2, D2, D3, D4, D5. D6, D7, D8, dan D9.
Rumus Desil
Dn= 1 +(n/10N – fkb)
Fi
Untuk data kelompok:
Dn= 1+ (n/10N- fkb) xi
Fi
Keterangan :
- Dn= desil yang ke-n (disini n dapat diisi dengan bilangan:1, 2, 3, 4, 5, 6, 7, 8, atau 9.
- 1= lower limit( batas bawah nyata dari skor atau interval yang mengandung desil ke-n).
- N= number of cases.
- Fkb= frekuensi kumulatif yang terletak dibawah skor atau interval yang mengandung desil ke-n.
- Fi= frekuensi dari skor atau interval yang mengandung desil ke-n, atau frekuensi aslinya.
- i=interval class atau kelas interval.
Contoh Perhitungan Cara Mencari Desil Bentuk Data Tunggal
Mencari desil data tunggal dengan cara mengurutkan data tersebut dari data terkecil sampai data terbesar atau sebaliknya. Kemudian posisi desil dicari dengan rumus:
Posisi Ds1 = 1/10 (n+1) Posisi Ds6 = 6/10 (n+1)
Posisi Ds2 = 2/10 (n+1) Posisi Ds7 = 7/10 (n+1)
Posisi Ds3 = 3/10 (n+1) Posisi Ds8 = 8/10 (n+1)
Posisi Ds4 = 4/10 (n+1) Posisi Ds9 = 9/10 (n+1)
Posisi Ds5 = 5/10 (n+1) Dimana: n = jumlah data
Contoh:
Diketahui data: 65; 70; 90; 40; 35; 45; 70; 80; 75; dan 50 Pertanyaan: Carilah letak (Ds2 dan Ds7)
Langkah-langkah menjawab:
1) Urutkan data terkecil sampai data terbesar
| No. Urut data | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Data | 35 | 40 | 45 | 50 | 65 | 70 | 70 | 75 | 80 | 90 |
2) Hitung dan cari posisi Desil (Ds2 dan Ds7) dengan rumus:
Posisi Ds2 = 2/10 (n+1) = 2/10 (10+1) = 2,2 artinya Desil 2,2 terletak pada posisi data ke-2,2. Apabila menemukan gejala semacam ini Ds2 dicari dengan cara:
Ds2 = data ke-2 + data 0,2 (data ke-3 – data ke-2)
= 40 + 0,2 (45 – 40) = 41 Jadi, posisi Ds2 berada pada nilai 41
Posisi DS7 = 7/10 (n+1) = 7/10 (10+1) = 7,7 artinya Desil 7,7 terletak pada posisi data ke-7,7. Apabila menemukan gejala semacam ini DS7 dicari dengan cara:
DS7 = data ke-7 + data 0,7 (data ke-8 – data ke-7)
= 70 + 0,7 (75 – 70) = 73,5 Jadi, Posisi DS7 berada pada nilai 73,5
Contoh Perhitungan Cara Mencari Desil Bentuk Data Berkelompok
Misalkan kita ingin mencari D3 dan D7 dari data yang tercantum pada table 3.12, proses perhitungannya adalah sebagai berikut:
Table 3.14. Perhitungan desil ke-3 dan desil ke-7 dari data yang tertera pada table 3.12.
| Nilai (x) | F | Fkb |
| 70-74
65-69 60-64 55-59 50-54 45-49 40-44 35-39 30-34 25-29 20-24 |
3
5 6 7 7 17 15 7 6 5 2 |
80
77 72 66 59 52 35 20 13 7 2 |
| Total | 80= N | – |
Mencari D3:
Titik D3= 3/10N= 3/10X80= 24 (terletak pada interval 40-44). Dengan demikian dapat kita ketahui: 1= 39,50; fi= 15, dan fkb= 20.
D3= 1 + (3/10N-fkb) xi=39,50 (24-20) x 5
Fi 15
= 39,50+ 20= 39,50 + 1,33= 40,83
15
Mencari D7:Ø
Titik D7= 7/10N= 7/10X80= 56 (terletak pada interval 50-54). Dengan demikian dapat kita ketahui: 1= 49,50; fi= 7, dan fkb= 52.
D7= 1 + (7/10N-fkb) xi=49,50 (50-54) x 5
Fi 7
= 49,50+ 20= 49,50 + 2,86= 40,83
Contoh lain untuk desil :
- Untuk data yang belum dikelompokkan
- Susunan berdasarkan urutan data dimulai dari data yang terkecil sampai terbesar
- Tentukan letak dari desil yang diminati letak D1 = data ke ;
Di = desil ke-i
i = 1,2,3,…..,9
n = banyaknya data
- Tentukan nilai dari desil yang diminati tersebut, misalkan nilai D1, nilai D3 ataupun nilai desil lainnya.
Misalnya untuk menentukan desil dari kumpulan data berikut:
- Data ganjil
12 8 10 22 18 4 9. Tentukan D,-nya!
Jawab:
Urutan datanya:
4 8 9 10 12 18 22
Letak desil (D3 = = 2,4) ada pada data yang ke-2,4
Atau nilai D3 nya = data kedua +0,4 (data ketiga –data kedua)
= 8+ 0,4 (10 -8) = 8,5
- Data genap
8 12 5 3 7 2 3 8
Urutkan data:
2 3 3 5 7 8 8 12 → Misal, menentukan nilai D2
maka:
Letak desil (D2 = = 1,8) ada pada data ke satu koma delapan
Nilai D2 = data kesatu + 0,8 (data kedua –data kesatu)
D2 = 2+0,8 (3-3) = 2
Pengertian Persentil
Persentil atau disingkat dengan (Ps) adalah nilai yang membagi data menjadi 100 bagian yang sama, setelah disusun dari data terkecil sampai data terbesar atau sebaliknya. Cara mencari Persentil hampir sama dengan mencari nilai Desil. Bedanya kalau Desil data dibagi 10 bagian yang sama, sedangkan Persentil data dibagi 100 bagian yang sama. Harga-harga Persentil ada 99 bagian, yaitu Ps1, sampai Ps9.
Menurut beberapa ahli yang mengemukakan pengertian mengenai persentil adalah sebagai berikut.
- Persentil adalah titik atau nilai yang membagi suatu distrubusi data menjadi seratus bagian yang sama besar (Sudijono, 2006: 99). Karena perrsentil sering disebut “ukuran per-ratus-an”. Titik yang membagi distribusi data ke dalam seratus bagian yang sama besar ialah titik-titik: P1, P2, P3, P4, P5, P6, . . . dan seterusnya, sampai dengan P99. Jadi didapat sebanyak 99 titik pesenti yang membagi seluruh distribusi data ke dalam seratus bagian yang sama besar, masing-masing sebesar 1/100 atau 1%.
- Persentil adalah suatu titik dalam distribusi yang menjadi batas satu persen (1%) dari frekuensi yang terbawah (Koyan, 2012: 22). Pesentil adalah nilai-nilai yang membagi sebagaian data atau suatu distribusi frekuensi menjadi 100 bagian yang sama (Wiriawan, 2001: 115).
Persentil yang biasa dilambangkan P, adalah titik atau nilai yang membagi suatu distribusi data menjadi seratus bagian yang sama besar. Karena itu persentil sering disebut ukuran perseratusan.
Titik yang membagi distribusi data ke dalam seratus bagian yang sama besar itu ialah titik-titik: P1, P2, P3, P4, P5, P6, … dan seterusnya, sampai dengan P99. jadi disini kita dapati sebanyak 99 titik persentil yang membagi seluruh distribusi data ke dalam seratus bagian yang sama besar, masing-masing sebesar 1/ 100N atau 1%, seperti terlihat pada kurva dibawah ini:
Rumus Persentil
Untuk data tunggal :
Pn= 1 +(n/10N – fkb)
Fi
Atau
| Letak Pi =
|
Keterangan:
Pi = Persntil ke-i
i = 1, 2, 3, … , 99
n = banyak data
Untuk data kelompok:
Pn= 1+ (n/10N- fkb) xi
Fi
Pn= persentil yang ke-n (disini n dapat diisi dengan bilangan-bilangan:1, 2, 3, 4, 5, dan seterusnya sampai dengan 99.
1= lower limit( batas bawah nyata dari skor atau interval yang mengandung persentil ke-n).
N= number of cases.
Fkb= frekuensi kumulatif yang terletak dibawah skor atau interval yang mengandung persentil ke-n.
Fi= frekuensi dari skor atau interval yang mengandung persentil ke-n, atau frekuensi aslinya.
i= interval class atau kelas interval.
Atau
Di = b + P
Keterangan :
Di = Desil ke-i
b = tepi bawah kelas Di
P = panjang kelas
n = banyak data
F = jumlah frekuensi sebelum kelas Di
f = frekuensi kelas Di
Tabel. 3.15. Perhitungan persentil ke-5, persentil ke-20 dan persentil ke-75 dari data yang tertera pada tabel 3.13.
| Nilai (x) | F | Fkb |
| 70-74
65-69 60-64 55-59 50-54 45-49 40-44 35-39 30-34 25-29 20-24 |
3
5 6 7 7 17 15 7 6 5 2 |
80
77 72 66 59 52 35 20 13 7 2 |
| Total | 80= N | – |
Contoh Cara Perhitungan desil untuk data tunggal
Misalkan kita ingin mencari persentil ke-5 (P5), persentil ke-20 (P20), dan ke-75 (P75),dari data yang disajikan pada tabel 3.13 yang telah dihitung desilnya itu. Cara menghitungnya adalah sebagai berikut:
Mencari persentil ke-5 (P5):
Titik P5= 5/10N= 5/10X60= 3 (terletak pada skor 36). Dengan demikian dapat kita ketahui: 1= 35,50; fi= 2, dan fkb= 1.
P5= 1 + (5/10N-fkb) =36,50 +(3-1)
Fi 2
= 36,50
Mencari persentil ke-75 (P75):
Titik P75= 75/10N= 75/10X60= 45 (terletak pada skor 42). Dengan demikian dapat kita ketahui: 1= 41,50; fi= 8, dan fkb= 40
P75= 1 + (75/10N-fkb) =41,50 +(45-40)
Fi 8
= 42,125
Contoh Cara Perhitungan mencari persentil untuk data kelompok
Misalkan kembali ingin kita cari P35 dan P95 dari data yang disajikan pada tabel 3.14.
Mencari persentil ke-35 (P35):
Titik P35= 35/100N= 35/100X80= 28 (terletak pada interval 40-44). Dengan demikian dapat kita ketahui: 1= 39,50; fi= 15, dan fkb= 20, i=5
P35= 1 + (35/100N-fkb) Xi =39,50 +(45-40) X 5
Fi 8
= 39,50+2,67
= 42,17
Mencari persentil ke-95 (P95):
Titik P95= 95/100N= 95/100X80= 76 (terletak pada interval 65-69). Dengan demikian dapat kita ketahui: 1= 64,50; fi= 5, dan fkb= 72, i=5
P95= 1 + (95/100N-fkb) Xi =64,50 +(65-69) X 5
Fi 5
= 64,50+4
= 68,50
Tabel 3.16. Perhitungan persentil ke-35 dan persentil ke-95 dari data yang tertera pada tabel 3.14.
| Nilai (x) | F | Fkb |
| 70-74
65-69 60-64 55-59 50-54 45-49 40-44 35-39 30-34 25-29 20-24 |
3
5 6 7 7 17 15 7 6 5 2 |
80
77 72 66 59 52 35 20 13 7 2 |
| Total | 80= N | – |
Kegunaan persentil dalam dunia pendidikan adalah:
- Untuk mengubah rawa score (raw data) menjadi standard score (nilai standar).
Dalam dunia pendidikan, salah satu standard score yang sering digunakan adalah eleven points scale ( skala sebelas nilai) atau dikenal pula dengan nama standard of eleven (nilai standard sebelas) yang lazim disingkat dengan stanel.
Pengubahan dari raw score menjadi stanel itu dilakukan dengan jalan menghitung: P1- P3- P8- P21- P39- P61- P79- P92- P97- dan P99.
Jika data yang kita hadapi berbentuk kurva normal (ingat: norma atau standar selalu didasarkan pada kurva normal itu), maka dengan 10 titik persentil tersebut diatas akan diperoleh nilai-nilai standar sebanyak 11 buah, yaitu nilai-nilai 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, dan 10.
- Persentil dapat digunakan untuk menentukan kedudukan seorang anak didik, yaitu: pada persentil keberapakah anak didik itu memperoleh kedudukan ditengah-tengah kelompoknya.
- Persentil juga dapat digunakan sebagai alat untuk menetapkan nilai batas lulus pada tes atau seleksi.
Misalkan sejumlah 80 orang individu seperti yang tertera pada tabel 3.16. itu hanya akan diluluskan 4 orang saja (=4/ 80 X 100%= 5%) dan yang tidak akan diluluskan adalah 76 orang (= 76X80 X 100%=95%), hal ini berarti bahwa P95 adalah batas nilai kelulusan. Mereka yang nilai-nilainya berada pada P95 kebawah, dinyatakan tidak lulus, sedangkan diatas P95 dinyatakan lulus. Dalam perhitungan diatas telah kita peroleh P95= 68,50; berarti yang dapat diluluskan adalah mereka yang nilainya diatas 68,50 yaitu nilai 69 ke atas.
1. Contoh Soal Kuartil Data Tunggal
- Data Tunggal
a. Tentukan Q1, Q2, dan Q3 dari data : 3, 4, 7, 8, 7, 4, 8, 4, 9, 10, 8, 3, 7, 12.
Jawab:
Data yang telah diurutkan: 3, 3, 4, 4, 4, 7, 7, 7, 8, 8, 8, 9, 10, 12.
Letak dari Qi dirumuskan sebagai berikut.
b. Dalam suatu tes terhadap 50 siswa didapat tabel frekuensi tunggal sebagai berikut.
| Nilai | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Frekuensi | 3 | 5 | 6 | 8 | 12 | 6 | 7 | 3 |
Berdasarkan data di atas, tentukan kuartil ke-2.
Jawab:
Jadi, kuartil ke-2 adalah 6.
2. Contoh Soal Kuartil Data Berkelompok
- Data Kelompok
Tentukan Q1 (kuartil bawah), Q2 (median), dan Q3 (kuartil atas) dari data tes Matematika terhadap 40 siswa kelas XI IPA berikut ini.
| Nilai | Frekuensi |
| 40 – 49
50 – 59 60 – 69 70 – 79 80 – 89 90 – 99 |
4
5 14 10 4 3 |
Keterangan: Qi = kuartil ke-i (1, 2, atau 3)
bi = tepi bawah kelas kuartil ke-i
N = banyaknya data
F = frekuensi kumulatif kelas sebelum kelas kuartil
l = lebar kelas
f = frekuensi kelas kuartil
3. Contoh Soal Desil Data Tunggal
- Data Tunggal
Diketahui data: 9, 10, 11, 6, 8, 7, 7, 5, 4, 5. Tentukan:
- desil ke-2
- desil ke-4
Jawab:
Data diurutkan: 4, 5, 5, 6, 7, 7, 8, 9, 10, 11
4. Contoh Soal Desil Data Berkelompok
- Data Kelompok
Diketahui data pada tabel data kelompok di bawah.
| x | f |
| 41 – 45
46 – 50 51 – 55 56 – 60 61 – 65 |
3
6 16 8 7 |
Dari data tersebut tentukan:
- desil ke-1
- desil ke-9
Jawab:
| x | f | F kumulatif |
| 41 – 45
46 – 50 51 – 55 56 – 60 61 – 65 |
3
6 16 8 7 |
3
9 25 33 40 |
5. Contoh Soal Persentil Data Tunggal
- Data Tunggal
Diketahui: 9, 10, 11, 6, 8, 7, 7, 5, 4, 5, tentukan persentil ke-30 dan persentil ke-75.
Jawab:
Data diurutkan: 4, 5, 5, 6, 7, 7, 8, 9, 10, 11
Letak persentil dirumuskan dengan:
6. Contoh Soal Persentil Data Kelompok
- Data Kelompok
Diketahui data pada tabel data kelompok di bawah.
| x | f |
| 41 – 45
46 – 50 51 – 55 56 – 60 61 – 65 |
3
6 16 8 7 |
Dari data tersebut tentukan:
- Persentil ke-25
- Persentil ke-60
Jawab:
| x | f | F kumulatif |
| 41 – 45
46 – 50 51 – 55 56 – 60 61 – 65 |
3
6 16 8 7 |
3
9 25 33 40 |
SIMPANGAN KUARTIL
SIMPANGAN KUARTIL/ JANGKAUAN SEMI ANTAR KUARTIL
Jangkauan Antar Kuartil adalah K3 – K1. atau dengan JAK = jangkauan antar kuartil, K3 = kuartil ke 3, K1 = kuartil ke 1.
NILAI STANDAR (z-SCORE)
Misal kita mempunyai sebuah sampel berukuran n (banyak datanya sama dengan n), dan datanya x1, x2, x3,…, xn. Rata-rata nya = x dan simpangan bakunya = s. Dibentuk data baru: z1, z2, z3,…, zn dengan menggunakan
KOEFISIEN VARIASI
KV =
JAK = K3 – K1
Jangkauan semi antar kuartil = 1/2 (K3 – K1)
KUARTIL Notasi: q
Kuartil membagi data (n) yang berurutan atas 4 bagian yang sama banyak.
——|——|——-|——-
Q1 Q2 Q3
Q1 = kuartil bawah (1/4n )
Q2 = kuartil tengah/median (1/2n)
Q3 = kuartil atas (1/4n )
Untuk data yang tidak dikelompokkan terlebih dahulu dicari mediannya, kemudian kuartil bawah dan kuartil atas.
Untuk data yang dikelompokkan rumusan kuartil identik dengan rumusan mencari median.
Q1 = L1 + [(1/4n – (å f)1)/fQ1] . c
Q3 = L3 + [(3/4n – (å f)3)/fQ3] . c
SIMPANGAN KUARTIL Notasi: Qd
(JANGKAUAN SEMI INTERKUARTIL) Qd = (Q3 – Q1) / 2
SIMPANGAN KUARTIL Notasi: Qd
(JANGKAUAN SEMI INTERKUARTIL) Qd = (Q3 – Q1) / 2
Simpangan kuartil / rentang semi antar kuartil
Simpangan Kuartil (Qd)
Contoh: Tentukan Qd dari: 2, 3, 4, 6, 6, 8, 8, 8, 10, 10, 10
Jawab: n=11
Q1 = n+1/4 = 3 (Data: 4)
Q3 = 3(n+1)/4 = 9 (Data: 10)
Qd = � (Q3 � Q1) = � x 6 =3
Contoh Soal Simpangan Kuartil
- Data tidak dikelompokkan
Diketahui data
95, 84, 86, 90, 93, 88, 97, 98, 89, 94
Data diurutkan terlebih dahulu, menjadi:
84 86 818 89 90 93 94 915 97 98
Q1 = 88 ; Q2 = 90 93 ; Q3 = 95
- Jangkauan J = 98 – 84 = 14
b. Kuartil Q1=88 ; Q2 = (90+93)/2 = 91,5 ; Q3 = 95
Simpangan kuartil = Qd = (95 – 88) / 2 = 3,5
c. Rata-Rata
= (88+86+88+89+90+93+95+97+98)/10 = 91,4
Simpangan baku = Ö(((84-91,4)² + …… + (98-91,4)²)/10) = 4,72 - Data dikelompokkan
| Skor | Titik Tengah | Frekuensi |
| 50-54 | 52 | 4 |
| 55-59 | 57 | 6 |
| 60-64 | 62 | 8 |
| 65-69 | 67 | 16 |
| 70-74 | 72 | 10 |
| 75-79 | 77 | 3 |
| 80-84 | 82 | 2 |
| 85-89 | 87 | 1 |
| n = 50 |
- Jangkauan = Titik tengah kelas tertinggi – Titik tengah kelas terendah = 87-52 =35
- Kuartil bawah (¼n )
Q1 = 59,5 + ((12,5 – 10)/8 . (5)) = 61,06
Kuartil bawah (¾n )
Q3 = 69,5 + (37,5 – 34)/10 . 5 = 71,25
Simpangan Kuartil
Qd = (Q3 – Q1) / 2 = (71,25 – 61,06) / 2 = 5,09
Jangkauan Semi antar kuartil = simpangan kuartil = Qd = ½H = ½(Q3-Q1)
Rata-rata
x = ((4)(52) + (6)(57) + … + (1)(870) / 50 = 66,4
Simpangan Baku
___________________________________
Ö((52-66,4)² + …… + (87-66,4)²)/50 = 7,58
Jangkauan Semi antar kuartil = simpangan kuartil = Qd = ½H = ½(Q3-Q1)
CATATAN:
- Bila pada suatu kumpulan data, setiap data ditambah / dikurangi dengan suatu bilangan, maka:
– nilai statistik yang berubah: Rata-rata, Median, Modus, Kuartil.
– nilai statistik yang tetap : Jangkauan, Simpangan Kuartil, Simpangan baku. - Bila pada suatu kumpulan data, setiap data dikali ldibagi dengan suatu bilangan, maka: semua nilai statistiknya berubah.