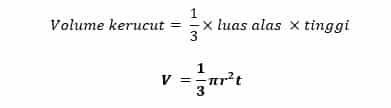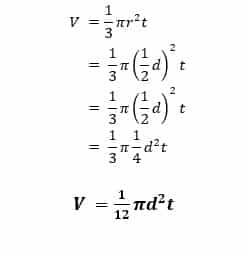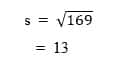Rumus Kerucut : Volume Luas Permukaan, Tinggi, Dan Gambar – Kerucut adalah bangun ruang yang dibatasi oleh sebuah sisi lengkung dan sebuah sisi alas berbentuk lingkaran. Definisi kerucut lainnya yaitu merupakan bangun ruang sisi lengkung yang menyerupai limas segi-n beraturan yang bidang alasnya berbentuk lingkaran.
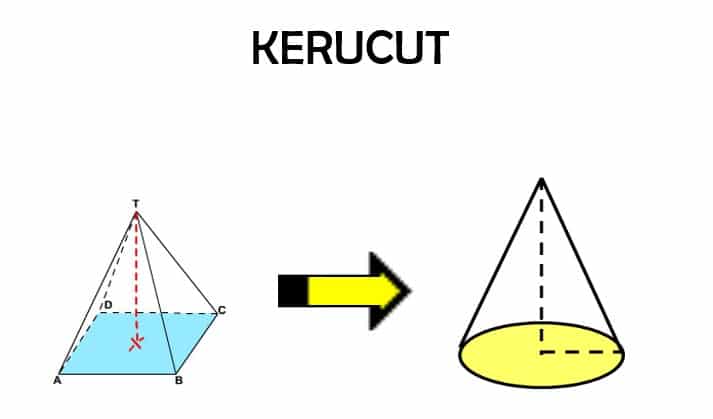
Kerucut dapat dibentuk dari sebuah segitiga siku-siku yang diputar sejauh 360o, di mana sisi siku-sikunya sebagai pusat putaran. Perhatikan gambar 1. Kerucut pada gambar 1 dapat dibentuk dari segitiga siku-siku TOA yang diputar, di mana sisi TO sebagai pusat putaran.
Baca Juga Artikel Yang Mungkin Berhubungan : 54 Gambar Jaring jaring Balok, Rumus, Dan Cara Membuat
Sifat Kerucut
Kerucut memiliki beberapa sifat, yaitu:
- Kerucut merupakan bangun ruang berbentuk limas yang alasnya berupa lingkaran
- Jaring-jaring kerucut terdiri dari lingkaran dan segi tiga
- Kerucut mempunyai 2 sisi dan 1 rusuk
- Satu sisi berbentuk bidang lengkung yang disebut selimut kerucut
- Mempunyai satu titik sudut
- Memiliki satu titik puncak
Jaring Jaring Kerucut
Berikut ini gambar jaring-jaring kerucut yang rumus hitung buat. Buat sobat hitung yang kesulitan mencari gambar jaring-jaring bangun ruang tersebut semoga gambar ini bisa membantu mengatasi kesulitan.
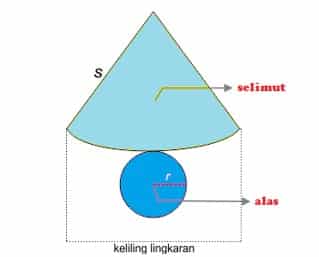
Jaring-jaring kerucut terdiri dari lingkaran sebagai alasnya dan bangun segitiga dengan alas lengkung yang merupakan selimutnya.
Unsur Unsur Kerucut
Kerucut memiliki unsur-unsur sebagai berikut:
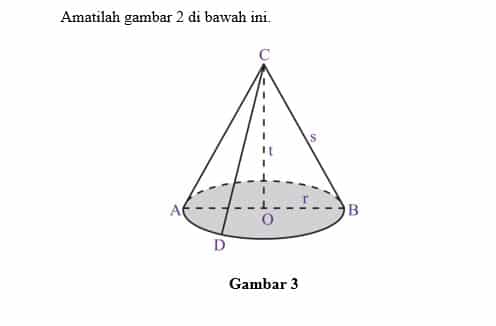
- Bidang alas, yaitu sisi yang berbentuk lingkaran (daerah yang diraster) dengan pusat di titik O.
- Diameter bidang alas (d), yaitu ruas garis AB.
- Jari-jari bidang alas (r), yaitu ruas garis OA dan ruas garis OB.
- Tinggi kerucut (t), yaitu jarak dari titik puncak kerucut C ke pusat bidang alas O, yakni ruas garis CO.
- Selimut kerucut, yaitu sisi kerucut yang tidak diraster yang merupakan bidang lengkung.
- Apotema atau garis pelukis (s), yaitu sisi miring BC.
Hubungan antara r, s, dan t pada kerucut dinyatakan dengan persamaan-persamaan berikut.
| s2 = r2 + t2 | r2 = s2 ─ t2 | t2 = s2 ─ r2 |
Volume Kerucut
Pada dasarnya kerucut merupakan limas karena memiliki titik puncak sehingga volume kerucut sama dengan volume limas, yaitu 1/3 kali luas alas kali tinggi. Oleh karena alas kerucut berbentuk lingkaran maka luas alasnya adalah luas lingkaran. Dengan demikian, volume kerucut dapat dirumuskan sebagai berikut.
Rumus Volume Kerucut
dengan
r = jari-jari lingkaran alas
t = tinggi kerucut
Karena r = 1/2 d (d adalah diameter lingkaran) maka bentuk lain rumus volume kerucut adalah sebagai berikut.
Contoh :
Baca Juga Artikel Yang Mungkin Berhubungan : Jaring Jaring Kubus : 11 Gambar Pola Dan Cara Membuat
Ciri ciri Bangun Ruang Kerucut
- Mempunyai 2 bidang sisi (1 bidang sisi lingkaran dan 1 bidang sisi selimut)
- Mempunyai 2 rusuk dan 1 titik sudut
Luas Permukaan Kerucut
Perlu kita ketahui bahwa, permukaan kerucut terdiri dari dua bidang, yaitu bidang lengkung (selimut) dan bidang alas berbentuk lingkaran. Untuk lebih jelasnya perhatikan uraian berikut.
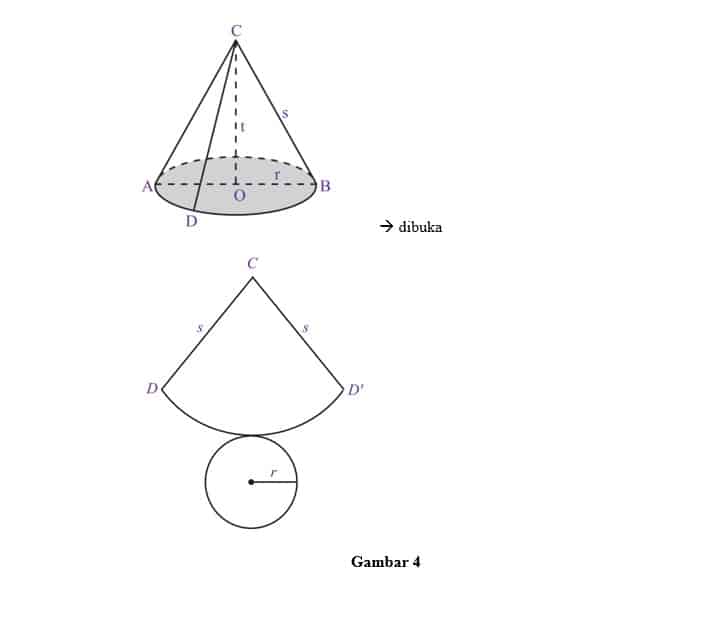
Jika kerucut di atas diiris sepangjang garis CD dan keliling alasnya, maka akan diperoleh jaring-jaring kerucut seperti pada gambar 3. Jaring-jaring kerucut ini terdiri atas:
- Juring lingkaran CDD’ yang merupakan selimut kerucut.
- Lingkaran dengan jari-jari r yang merupakan sisi alas kerucut.
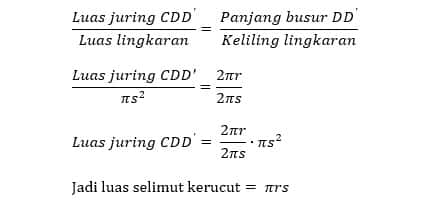
Misalnya panjang apotema adalah s dan jari-jari lingkaran alas adalah r. Selimut kerucut merupakan juring lingkaran berjari-jari s dengan panjang busur DD’ merupakan keliling lingkaran alas kerucut yaitu 2πr.
*) Dengan demikian kita peroleh
Rumus luas selimut kerucut
sama dengan luas juring CDD’.
*) Rumus Luas permukaan kerucut
= Luas selimut + Luas alas
dengan:
r : jari-jari lingkaran alas
s : apotema
π = 22/7 atau 3,14
Contoh Soal Luas Permukaan Kerucut :
- Sebuah kerucut mempunyai panjang jari-jari alasnya 6 cm dan tingginya 8 cm. Hitunglah luas permukaan kerucut tersebut ( π = 3,14).
Jawab :
Diketahui:
Jari-jari alas = r = 6cm
Tinggi kerucut = t = 8 cm
Ditanya: Luas permukaan kerucut
Penyelesaian:
- Jika diameter sebuah kerucut adalah 10 cm dan tingginya 12 cm, tentukan:
a. panjang apotema (s),
b. luas selimut kerucut,
c. luas permukaan
Jawab:
Diketahui :
d = 10 maka r = 5 cm
t = 12 cm
Ditanyakan :
a. panjang garis pelukis (s)
b. luas selimut kerucut
c. luas permukaan kerucut
Penyelesaian:
a. s2 = t2 + r2
= 122 + 52
= 144 + 25
= 169
Jadi, panjang garis pelukis kerucut tersebut adalah 13 cm.
b. Luas selimut kerucut = πrs
= 3,14 x 5 x 13
= 204,1
Jadi, luas selimut kerucut tersebut adalah 204,1 cm2.
c. Luas permukaan kerucut = πr (s + r)
= 3,14 x 5 x (13 + 5)
= 282,6
Jadi, luas permukaan kerucut tersebut adalah 282,6 cm2
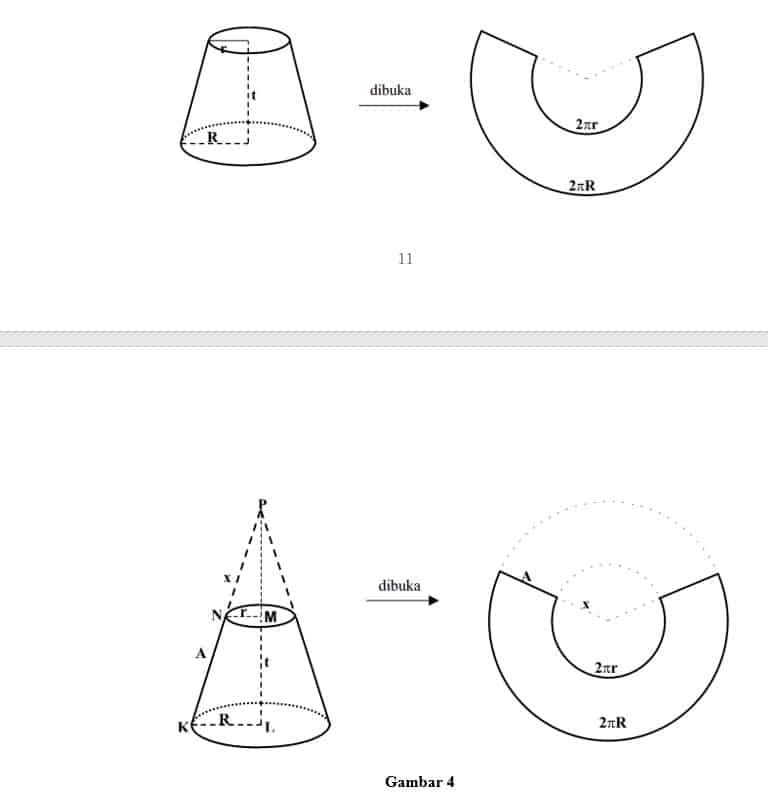
Luas Kerucut Terpancung
Luas selimut kerucut terpancung adalah luas kerucut besar dikurangi luas selimut kerucut kecil. Perhatikan gambar 4 berikut ini.
Jadi
Rumus Luas Kerucut Terpancung
Contoh :
Jawaban :
Volume Kerucut Terpancung
Volume kerucut terpancung adalah volume kerucut besar dikurangi volume kerucut kecil. Perhatikan gambar 5 di bawah ini.
Contoh Gambar Bangun Kerucut Dalam Kehidupan
DAFTAR PUSTAKA
-
Handoko, Tri,Terampil Matematika.jakarta:Untuk Kelas 5 Sekolah Dasar,2004
-
http://www.scribd.com/doc/91362394/Kerucut
-
Djoko Iswadji 1988. Geometri ruang Yogyakarta : FMIPA IKIP Yogyakarta.