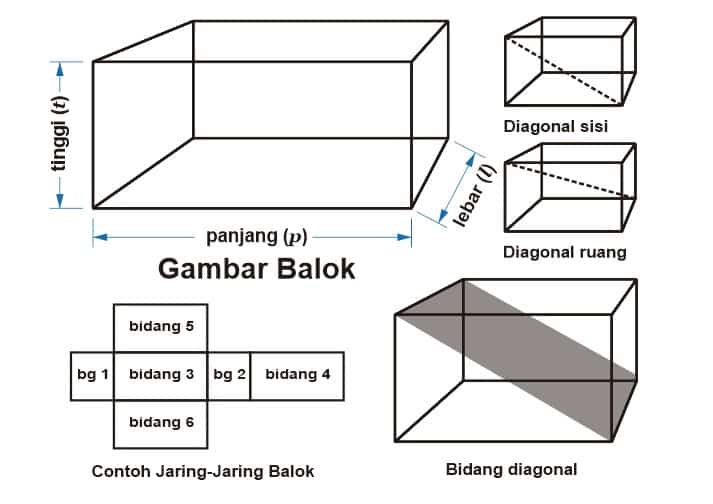
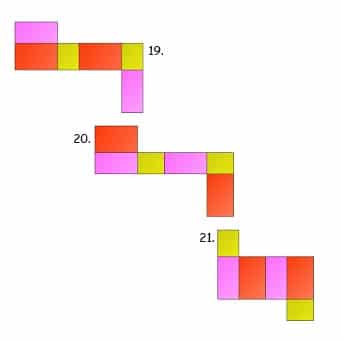
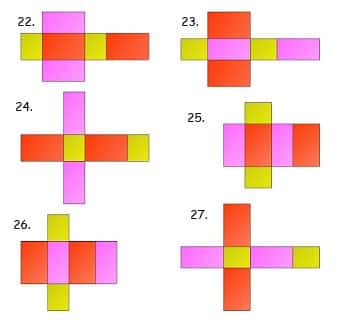
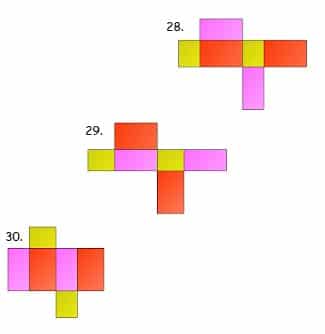
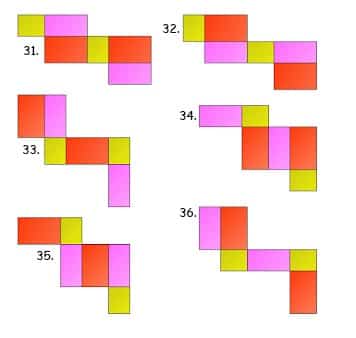
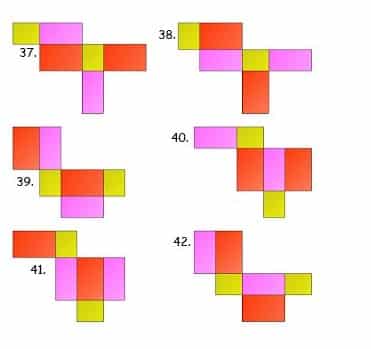
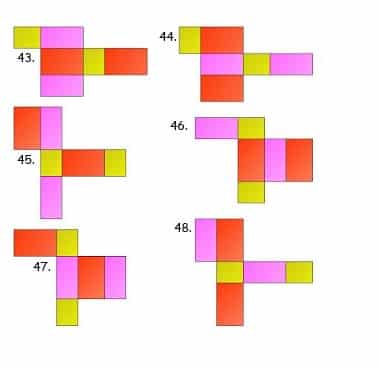
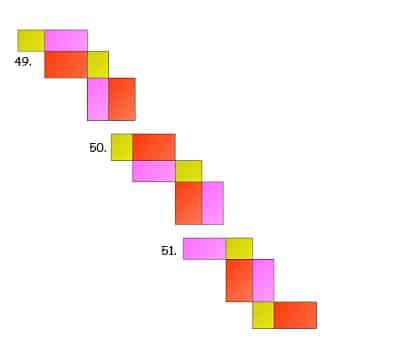
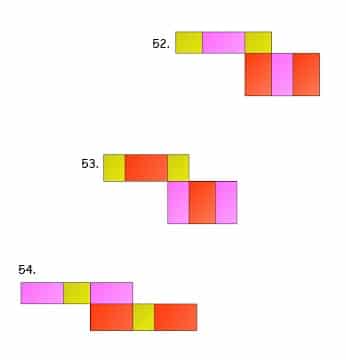
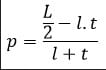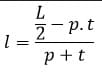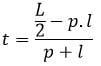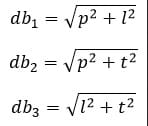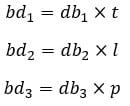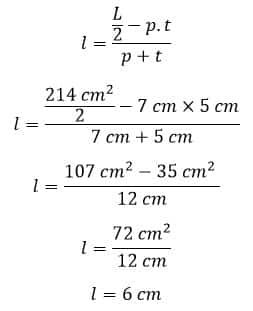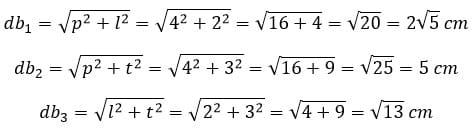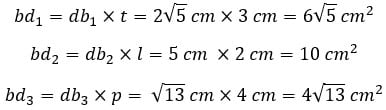Sahabat gurupendidikan, Jaring jaring adalah bentuk asli dari bangun ruang yang telah dilakukan pembelahan. Atau pengertian lain dari jaring-jaring adalah sebuah bangun datar yang apabila dikaitkan akan membentuk sebuah bangun ruang.
PENGERTIAN JARING JARING BALOK
jaring-jaring balok adalah hasil berupa satuan bangun yang merupakan pembelahan dari bangun ruang berupa balok.
Ciri Ciri Balok
- Memiliki 12 rusuk
- 8 titik sudut
- Terdiri dari 6 sisi
- Seluruh sudutnya pasti berbentuk siku-siku;
- Mempunyai 12 diagonal bidang dan 4 diagonal dalam bentuk bangun ruang
Baca Juga : Jaring Jaring Kubus : 11 Gambar Pola, Contoh Soal
Sifat-Sifat Balok dan Bagian Balok
Berikut sifat-sifat umum balok:
- Balok tersusun dari 3 pasang sisi yang sama (total 6 buah sisi).
- Setiap sisi berbentuk segiempat yaitu persegi atau persegi panjang.
- Paling sedikit harus mempunyai 1 pasang sisi dengan bentuk yang berbeda.
- Mempunyai 12 rusuk.
- Rusuk-rusuk yang sejajar mempunyai ukuran yang sama.
- Mempunyai 4 diagonal bidang.
- Diagonal bidang yang sejajar mempunyai ukuran yang sama.
- Mempunyai 4 diagonal ruang dan semuanya mempunyai ukuran yang sama.
- Setiap bidang diagonal berbentuk persegi panjang.
Baca Juga Artikel Yang Mungkin Berhubungan : Rumus Kerucut : Volume Luas Permukaan, Tinggi, Dan Gambar
Rumus Balok
- t = tinggi, p = panjang, l = lebar
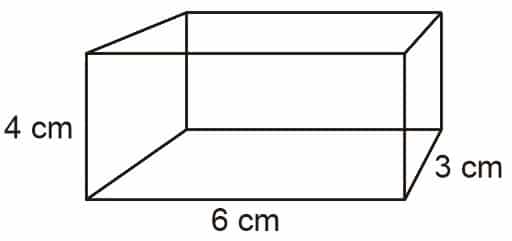
Contoh 1 : Menghitung Volume dan Luas Permukaan Balok
Hitunglah volume dan luas permukaan balok berikut!
Diketahui:
p = 6 cm
l = 3 cm
t = 4 cm
Ditanya:
Volume (V) dan Luas Permukaan (L) Balok
Penyelesaian:
V = p × l × t
V = 6 cm × 3 cm × 4 cm
V = 72 cm³
L = 2 × (p.l + p.t +l.t)
L = 2 × ((6 cm × 3 cm) + (6 cm × 4 cm) + (3 cm × 4 cm))
L = 2 × (18 cm² + 24 cm² + 12²)
L = 2 × 54 cm²
L = 108 cm²
Jadi, volume balok adalah 72 cm³ dan luas permukaan balok adalah 108 cm².
Contoh 2: Cara Menghitung Panjang Balok Jika Diketahui Luas Permukaannya
Sebuah balok mempunyai luas permukaan 52 cm², jika diketahui lebar balok 2 cm dan tinggi balok 3 cm. Hitunglah panjang balok tersebut!
Diketahui:
L = 52 cm²
l = 2 cm
t = 3 cm
Ditanya:
Panjang balok (p)
Penyelesaian:
Jadi, panjang balok adalah 5 cm.
Contoh 3: Cara Menghitung Panjang Balok Jika Diketahui Volume
Sebuah balok mempunyai volume 12 cm³, jika diketahui lebar balok 2 cm dan tinggi balok 2 cm. Hitunglah panjang balok tersebut!
Diketahui:
V = 12 cm³
l = 2 cm
t = 2 cm
Ditanya:
Panjang balok (p)
Penyelesaian:
p = V ÷ l ÷ t
p = 12 cm³ ÷ 2 cm ÷ 2 cm
p = 3 cm
Jadi, panjang balok adalah 3 cm.
Contoh 4: Cara Menghitung Lebar Balok Jika Diketahui Luas Permukaannya
Sebuah balok mempunyai luas permukaan 214 cm², jika diketahui panjang balok 7 cm dan tinggi balok 5 cm. Hitunglah lebar balok tersebut!
Diketahui:
L = 214 cm²
p = 7 cm
t = 5 cm
Ditanya:
Lebar balok (l)
Penyelesaian:
Jadi, lebar balok adalah 6 cm.
Contoh 5: Cara Menghitung Lebar Balok Jika Diketahui Volume
Sebuah balok mempunyai volume 336 cm³, jika diketahui panjang balok 8 cm dan tinggi balok 6 cm. Hitunglah lebar balok tersebut!
Diketahui:
V = 336 cm³
p = 8 cm
t = 6 cm
Ditanya:
Lebar balok (l)
Penyelesaian:
l = V ÷ p ÷ t
l = 336 cm³ ÷ 8 cm ÷ 6 cm
l = 7 cm
Jadi, panjang lebar adalah 7 cm.
Contoh 6: Cara Menghitung Tinggi Balok Jika Diketahui Luas Permukaannya
Sebuah balok mempunyai luas permukaan 382 cm², jika diketahui panjang balok 9 cm dan lebar balok 8 cm. Hitunglah tinggi balok tersebut!
Diketahui:
L = 382 cm²
p = 9 cm
l = 8 cm
Ditanya:
Tinggi balok (l)
Penyelesaian:
Jadi, tinggi balok adalah 7 cm.
Contoh 7: Cara Menghitung Tinggi Balok Jika Diketahui Volume
Sebuah balok mempunyai volume 7120 cm³, jika diketahui panjang balok 10 cm dan lebar balok 8 cm. Hitunglah tinggi balok tersebut!
Diketahui:
V = 720 cm³
p = 10 cm
l = 8 cm
Ditanya:
Tinggi balok (l)
Penyelesaian:
l = V ÷ p ÷ l
l = 720 cm³ ÷ 10 cm ÷ 8 cm
l = 9 cm
Jadi, panjang lebar adalah 9 cm.
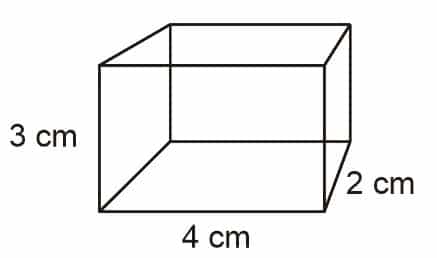
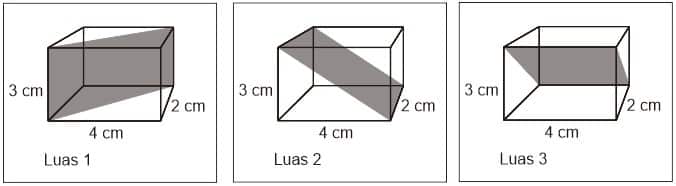
Contoh 8: Menghitung Diagonal Bidang, Diagonal Ruang, dan Luas Bidang Diagonal
Hitunglah panjang diagonal bidang, diagonal ruang, dan luas bidang diagonal balok di bawah!
Diketahui:
p = 4 cm
l = 2 cm
t = 3 cm
Penyelesaian:
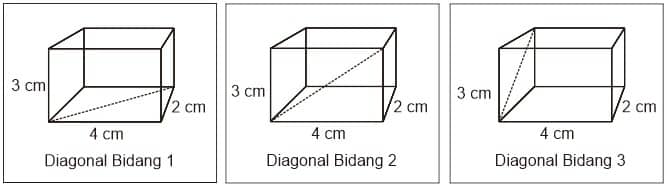
Panjang diagonal bidang
Balok mempunyai 12 diagonal bidang dan dibagi menjadi 3 kelompok diagonal bidang
Dengan panjang masing-masing, dapat dihitung menggunakan rumus Pythagoras
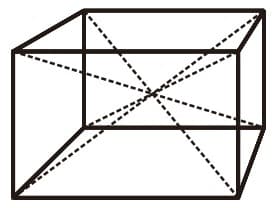
Panjang diagonal ruang
Balok mempunyai 4 diagonal ruang yang sama panjang
Dengan panjang setiap diagonal ruang
Luas bidang diagonal
Balok mempunyai 3 pasangan luas bidang diagonal (total 6 bidang diagonal):
Dengan luas setiap bidang diagonal
Rumus Balok | Rumus Volume Balok dan Rumus Luas Permukaan Balok. 19 Mei 2019. <https://www.advernesia.com/blog/matematika/rumus-balok-rumus-volume-balok-dan-rumus-luas-permukaan-balok/>
Baca Juga : Rumus Volume Tabung : Luas Permukaan, Luas Selimut, Tinggi, & Contoh Soal
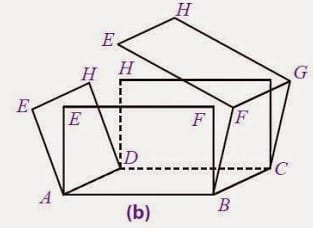
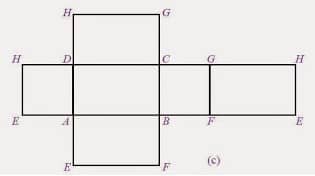
Cara Membuat Jaring-jaring Balok
Untuk lebih memantapkan pemahaman tentang jaring-jaring balok, kita akan mencoba praktek membuat jaring-jaring balok.
Ambil sebuah kardus yang berbentuk balok
Gunting kardus sesuai pola dari kubus pada titik-titik tertentu. Jangan sampai sisakan satu sisi bawah dan satu sisi samping.
Maka akan kamu dapatkan bentuk berupa jaring-jaring balok seperti gambar di atas.
Setelah kita membelah kotak kardus menjadi sebuah jaring-jaring balok, maka dapat kita ketahui bahwa jaring-jaring balok tersusun dari 6 buah persegi panjang yang terdiri dari 3 persegi panjang yang sama besar. Maka
- Persegi panjang ABCD sama dengan EFGH.
- Persegi panjang EHDA sama dengan BCGF.
- Persegi panjang ABFE sama dengan DCGH.
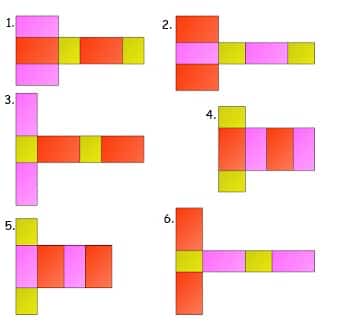
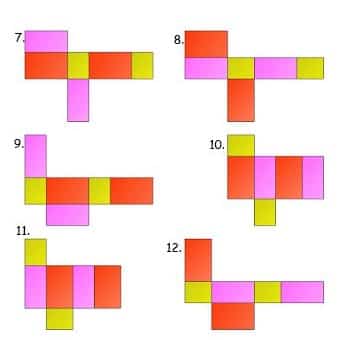
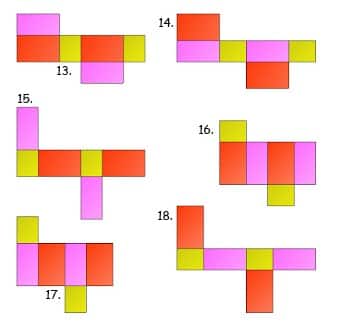
54 Contoh Gambar Jaring-jaring Balok
Demikian penjelasan tentang materi balok semoga dapat bermanfaat.