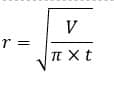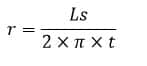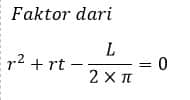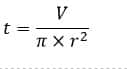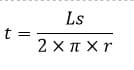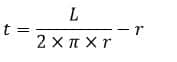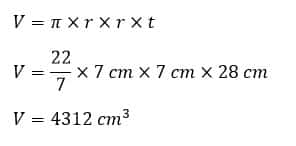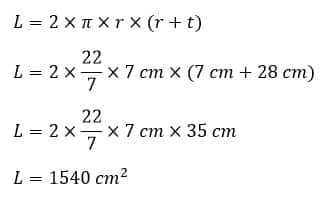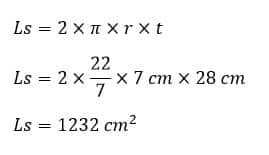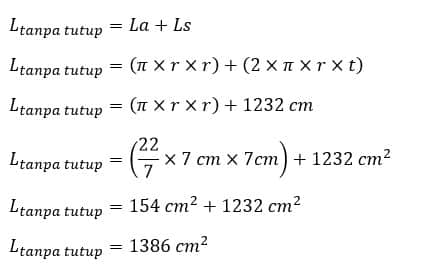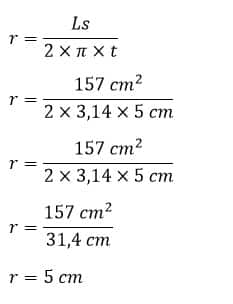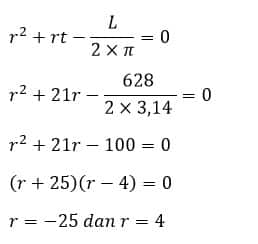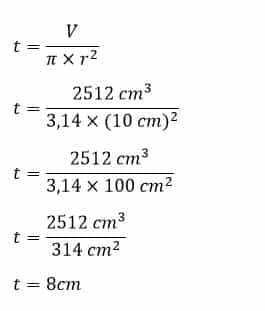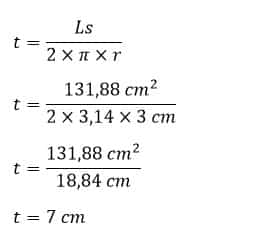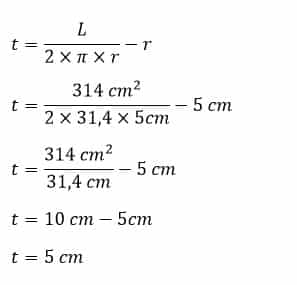Dalam matematika terdapat beberapa bangun ruang salah satunya adalah Tabung. Tabung merupakan bangun ruang yang dibatasi oleh dua sisi yang kongruen dan sejajar yang berbentuk lingkaran serta sebuah sisi lengkung. Banyak yang belum memahami dengan baik tentang penyelesaian masalah tabung, baik dari Definisi, unsur-unsur dan Penentuan Rumus-rumus Pada tabung. Penulis mengangkat makalah yang berjudul “Tabung” untuk memahami lebih jelas lagi tentang Tabung.
Baca Juga Artikel Yang Mungkin Berhubungan : Rumus Kerucut : Volume Luas Permukaan, Tinggi, Dan Gambar
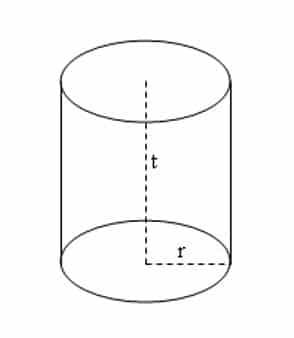
Pengertian Bangun Ruang (Tabung)
Tabung adalah bangun ruang yang dibatasi oleh dua bidang yang berbentuk lingkaran sebagai sisi alas dan sisi atas dan sebuah bidang lengkung yang merupakan sisi tegak yang disebut selimut tabung.
Sifat sifat Tabung
- Memiliki 2 sisi berbentuk lingkaran dan 1 sisi
berbentuk bidang lengkung (selimut tabung) - Memiliki 2 rusuk lengkung
- Tidak memiliki titik sudut
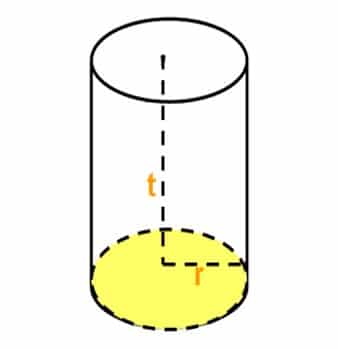
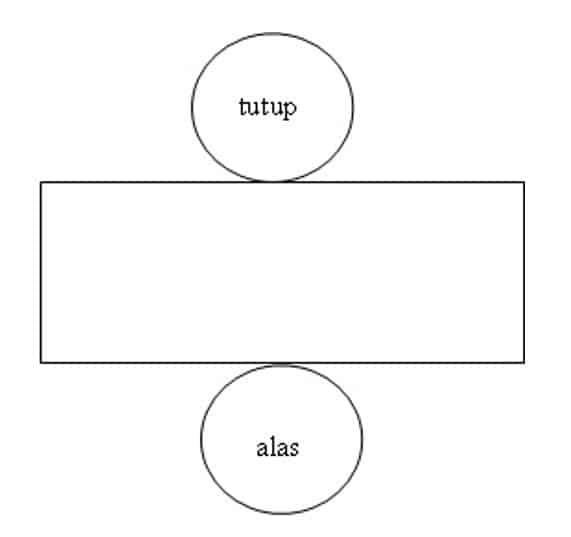
Gambar Tabung
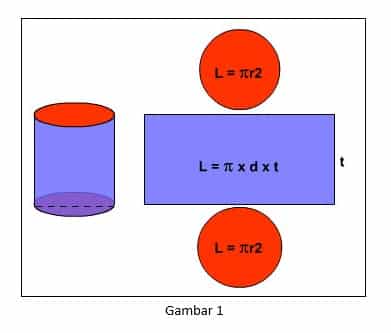
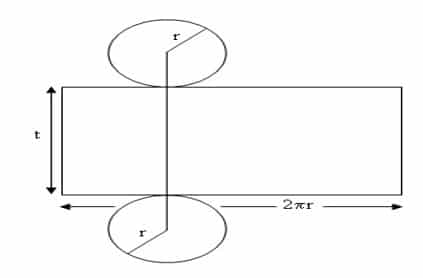
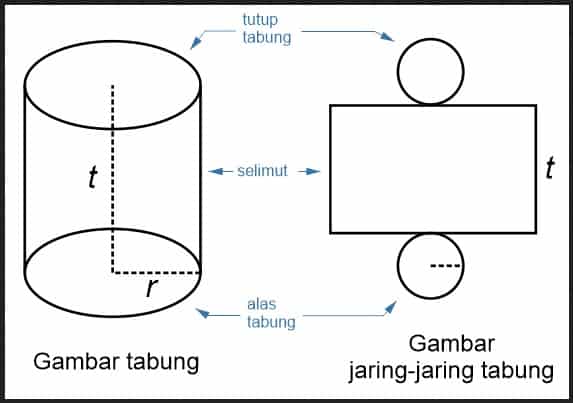
Bila Tabung dibuka baguan sisi atas dan sisi alasnya serta dipotong sepanjang garis lurus pada selimutnya dan diletakkan pada bidang datar, maka didapat jaring-jaring tabung, seperti Gambar 1.
- Bidang alas dan bidang atas berupa lingkaran dengan jari – jari yang sama.
- Tinggi tabung adalah jarak antara titik pusat lingkaran alas dan titik pusat lingkaran atas.
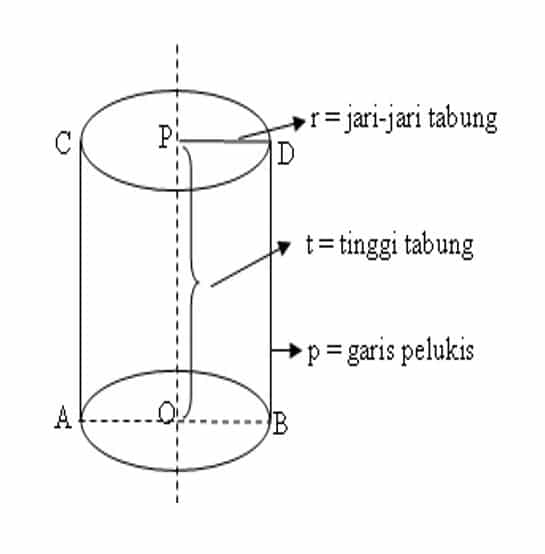
Unsur unsur Tabung
- Tabung mempunyai 3 sisi yaitu sisi atas, sisi bawah dan sisi lengkung/sisi tegak (yang selanjutnya disebut selimut tabung). Sisi alas dan sisi atas (tutup) berbentuk lingkaran yang kongruen (sama bentuk dan ukurannya).
- Tabung mempunyai 2 rusuk yang masing-masing berbentuk lingkaran.
- Tabung tidak mempunyai titik sudut.
Jarak antara bidang atas dan bidang bawah tabung disebut tinggi dari tabung itu.
Baca Juga Artikel Yang Mungkin Berhubungan : 54 Gambar Jaring jaring Balok, Rumus, Dan Cara Membuat
Cara Membuat Tabung Sederhana
Tabung merupakan bangun ruang yang terbentuk dari beberapa bangun datar. Saat ini banyak prodak yang menggunakan bentuk Tabung sebagai variasi untuk produk mereka. Contohnya seperti Sarden ABC dan masih banyak lagi.
Berikut adalah tahap-tahap pembuatn Tabung sederhana ;
- Siapkan beberapa bangun datar, yaitu 2 lingkaran yang keduanya mempunyai sama sisi dan 1 persegi panjang yang mempunyai panjang yang sama dengan keliling lingkaran.
- Sambungkan kedua sisi lebar pada Persegi Panjang dengan menggunakan alat perekat (Lem, Doubletip, dll). Lalu pasangkan kedua lingkaran disisi kosong yang ada pada Persegi Panjang yang sudah dibentuk seperti Gambar 3.
- Gambar 4 adalah hasilnya.
Baca Juga Artikel Yang Mungkin Berhubungan : Jaring Jaring Kubus : 11 Gambar Pola Dan Cara Membuat
Luas Permukaan Tabung
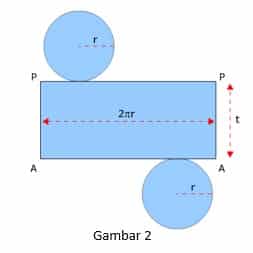
Luas permukaan tabung dapat kita lihat dari jaring-jaring tabung yang terdiri dari sebuah daerah persegi panjang dan dua daerah lingkaran yang kongruen. Daerah persegi panjang itu panjangnya sama dengan keliling lingkaran alas/atas dari tabung, sedang lebarnya sama dengan tinggi tabung.
Luas persegi panjang ini disebut luas bidang lengkung tabung. Jika r jari-jari tabung dan t adalah tinggi tabung, maka:
Rumus Luas Tabung
Luas Bidang Lengkung Tabung = Luas Persegi Panjang
= p x l
= Keliling lingkaran x tinggi tabung
= (2π) x (t)
= 2π r t
Luas Seluruh Permukaan Tabung = Luas Seluruh Bidang Sisi Tabung
= Luas Bidang Lengkung Tabung + 2 Luas Alas (Lingkaran)
= 2πrt + 2 (πr2)
= 2πr (r + t)
Baca Juga Artikel Yang Mungkin Berhubungan : Flowchart Adalah : Simbol Flowchart, Contoh, Dan Cara Membuatnya
Rumus Tabung
t = tinggi
jari-jari (r) = d÷2
diameter (d) = 2×r
π = 22/7 untuk jari-jari kelipatan 7 dan 3,14 untuk jari-jari bukan kelipatan 7
| Nama | Rumus |
|---|---|
| Volume (V) | V = π × r × r × t |
| V = π × r² × t | |
| Luas Permukaan (L) | L = 2 × π × r × (r + t) |
| Luas Selimut (Ls) | Ls = 2 × π × r × t |
| Ls = π × d × t | |
| Luas alas (La) | La = π × r × r |
 |
 |
| Jari-jari (r) diketahui Volume | 
|
| Jari-jari (r) diketahui Luas Selimut | 
|
| Jari-jari (r) diketahui Luas Permukaan | 
|
| Tinggi (t) diketahui Volume | 
|
| Tinggi (t) diketahui Luas Selimut | 
|
| Tinggi (t) diketahui Luas Permukaan | 
|
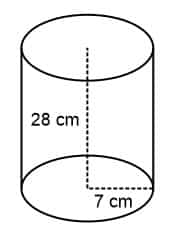
Contoh 1: Cara Menghitung Volume Tabung, Luas Permukaan Tabung, Luas Selimut Tabung, dan Luas Permukaan Tanpa Tutup
Hitunglah volume tabung, luas permukaan, dan luas selimut tabung berikut!
Diketahui:
t = 28 cm
r = 7 cm
Ditanya:
a) Volume tabung, b) Luas permukaan, c) Luas selimut, d) Luas permukaan tanpa tutup
Penyelesaian:
a) Rumus Dan Cara Menghitung volume tabung
b) Rumus Dan Cara Menghitung luas permukaan tabung
Luas permukaan tabung = Luas Selimut + Luas Alas + Luas Tutup
c) Rumus Dan Cara Menghitung luas selimut tabung
d) Rumus Dan Cara Menghitung luas permukaan tanpa tutup
Luas permukaan tanpa tutup = Luas selimut + Luas alas
Contoh 2: Rumus Dan Cara Menghitung Jari-Jari Tabung Jika Diketahui Volume Tabung
Hitunglah jari-jari tabung yang mempunyai tinggi 8 cm dan volume 2512 cm³!
Diketahui:
t = 8 cm
V = 2512 cm³
Ditanya:
Jari-jari tabung (r)
Penyelesaian:
Jadi, jari-jari tabung adalah 10 cm.
Contoh 3: Rumus Dan Cara Menghitung Jari-Jari Tabung Jika Diketahui Luas Selimut
Hitunglah jari-jari tabung yang mempunyai tinggi 5 cm dan luas selimut 157 cm²!
Diketahui:
t = 5 cm
Ls = 157 cm
Ditanya:
Jari-jari tabung (r)
Penyelesaian:
Jadi, jari-jari tabung adalah 5 cm.
Contoh 4: Rumus Dan Cara Menghitung Jari-Jari Tabung Jika Diketahui Luas Permukaan
Hitunglah jari-jari tabung yang mempunyai tinggi 21 cm dan luas permukaan 628 cm²!
Diketahui:
t = 21 cm
L = 628 cm²
Ditanya:
Jari-jari tabung (r)
Penyelesaian:
Jari-jari tabung memenuhi persamaan berikut
Dari hasil faktor persamaan dapat diuji
r = -25 cm tidak memenuhi syarat, karena hasil luas permukaan akan bernilai negatif atau tidak sama 628 cm².
r = 4 cm memenuhi syarat, karena hasil hasil luas permukaan bernilai 628 cm².
Jadi, jari-jari tabung tersebut adalah 4 cm.
Contoh 5: Rumus Dan Cara Menghitung Tinggi Tabung Jika Diketahui Volume
Hitunglah tinggi tabung yang mempunyai jari-jari 10 cm dengan volume 2512 cm³!
Diketahui:
r = 10 cm
V = 2512 cm³
Ditanya:
Tinggi tabung (t)
Penyelesaian:
Jadi, tinggi tabung 8 cm.
Contoh 6: Rumus Dan Cara Menghitung Tinggi Tabung Jika Diketahui Luas Selimut
Hitunglah tinggi tabung yang mempunyai jari-jari 3 cm dengan luas selimut 131,88 cm²!
Diketahui:
r = 3 cm
Ls = 131,88 cm²
Ditanya:
Tinggi tabung (t)
Penyelesaian:
Jadi, tinggi tabung adalah 7 cm.
Contoh 7: Rumus Dan Cara Menghitung Tinggi Tabung Jika Diketahui Luas Permukaan
Hitunglah tinggi tabung yang mempunyai jari-jari 5 cm dengan luas permukaan 314 cm²
Diketahui:
r = 5 cm
L = 314 cm²
Ditanya:
Tinggi tabung (t)
Penyelesaian:
Jadi, tinggi tabung adalah 5 cm.
Jaring jaring Tabung
Jika sebuah model peraga dari sebuah tabung yang terbuat dari kertas atau karton kita potong sepanjang salah satu garis pelukis dan keliling bidang alas dan bidang atasnya, kemudian kita buka sehingga terletak bersama pada sebuah bidang datar maka kita akan peroleh jaring-jaring dari tabung yang terdiri dari sebuah daerah persegi panjang (bidang lengkung tabung tadi) dan dua daerah lingkaran yang kongruen.
Volume Tabung
Untuk menentukan volume tabung, maka tabung kita pandang sebagai bangun yang terjadi dari sebuah prisma beraturan yang banyaknya sisi tak terhingga, sehingga keliling dari luas bidang alasnya sangat mendekati keliling dan luas sebuah lingkaran, sedangkan tinggi prisma itu menjadi tinggi dari tabung tersebut.
Dengan perkataan lain :
Volume sebuah silinder sama dengan limit volume prisma beraturan yang banyaknya sisi bertambah menjadi tak berhingga.
Jika r adalah jari-jari bidang alas tabung (bidang alas berupa lingkaran) dan t adalah tinggi tabung, maka :
Rumus Volume Tabung
Volume Tabung = Volume Prisma
= Luas Alas x Tinggi
= (pr2) x (t)
= p r 2 t
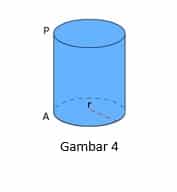
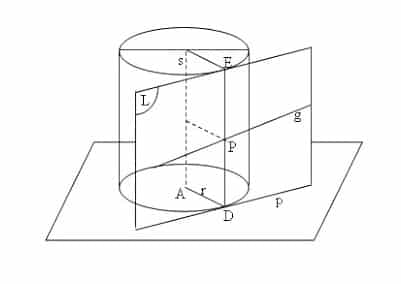
Bidang Singgung Pada Bidang Tabung
Pada gambar di atas, A merupakan pusat lingkaran alas dari tabung. Dibuat garis singgung pada p pada alas tabung itu dengan D sebagai titik singgung. Dibuat garis pelukis DE, maka bidang yang melalui P dan DE disebut bidang singgung pada bidang tabung. Jika dalam bidang singgung pada bidang tabung itu kita lukis garis g yang tidak sejajar dengan garis pelukis, maka garis g itu akan memotong garis pelukis DE di sebuah titik P yang merupakan titik persekutuan dari garis g dan bidang tabung.
Dalam hal ini maka garis g dikatakan menyinggung bidang tabung di titik P. Garis g juga merupakan garis yang menyilang sumbu tabung pada jarak tetap, yaitu r.
Karena bidang singgung L melalui garis pelukis yang letaknya selalu sejajar dengan sumbu tabung s, maka akibatnya bahwa setiap bidang singgung pada bidang tabung letaknya pasti sejajar dengan sumbu tabung s.
Dari pernyataan di atas dapatlah disimpulkan bahwa:
- Semua garis yang menyilang sebuah garis s dengan jarak tetap (r) terletak pada sebuah bidang yang menyinggung bidang tabung dengan s sebagai sumbu dan r sebagai jari-jarinya.
- Setiap bidang yang sejajar dengan sebuah garis s dan mempunyai jarak tetap (r) terhadap s, menyinggung bidang tabung dengan s sebagai sumbu dan r sebagai jari-jarinya.
Contoh Soal Volume Tabung
Seorang penjual minyak memiliki sebuah drum berbentuk tabung yang ia gunakan untuk menyimpan minyak dagangannya. Jari-jari alas yang dimiliki drum itu adalah 70cm dan memiliki tinggi 100cm. Berapa liter minyak yang dapat ditampung dalam drum tersebut?
