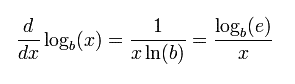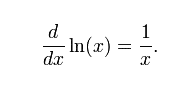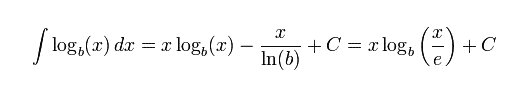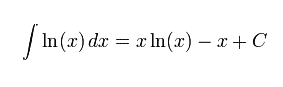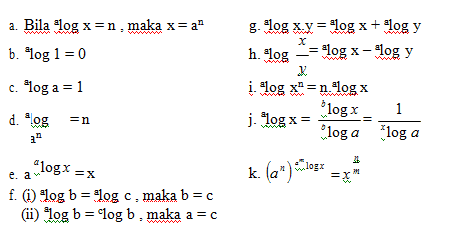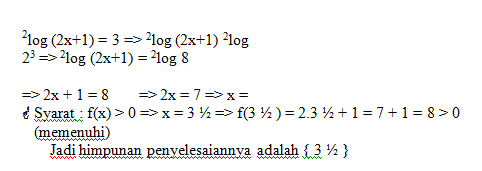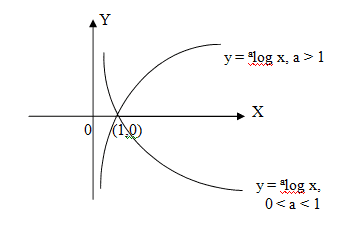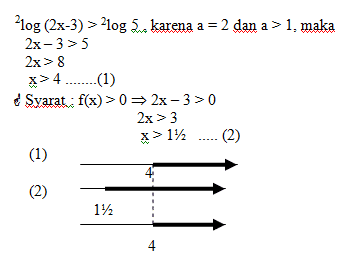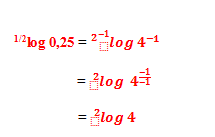Logaritma : Rumus, Sifat, Fungsi, Persamaan dan Contoh Soal – Belakangan ini, ilmu matematika telah berkembang pesat. Bukan hanya sebatas hitung menghitung menggunakan skala statistik, nilai, angka-angka real, kalkulus dan peluang. Akan tetapi, perkembangan ilmu matematika juga terjadi didasarkan pada penalaran-penalaran yang logis atas sistem matematis.
Baca Juga Artikel yang Mungkin Berhubungan : 17 Pengertian Matematika Menurut Para Ahli Beserta Bidangnya
Penalaran yang dilakukan oleh para ahli matematik diperoleh atas realita kehidupan yang nyata yang dirasakan oleh manusia. Perkembangan dan aplikasi dan bagian matematik ini sangat dirasakan oleh manusia di berbagai kehidupan. Penalaran inilah dalam bahasa matematika sering disebut logika.
Pengertian Logaritma
Logaritma adalah operasi matematika yang merupakan kebalikan dari eksponen atau pemangkatan.
Sejarah Logaritma
Ditinjau dari asal usul kata-katanya, kata Algoritma mempunyai sejarah yang agak aneh. Orang hanya menemukan kata Algorism yang berarti proses menghitung dengan angka Arab.
Seseorang dikatakan ”Algorist” jika menghitung menggunakan angka Arab. Para ahli bahasa berusaha menemukan asal kata ini namun hasilnya kurang memuaskan. Akhirnya para ahli sejarah matematika menemukan asal kata tersebut yang berasal dari nama penulis buku Arab terkenal, yaitu Abu Abdullah Muhammad Ibnu Musa Al-Khuwarrismi dibaca oleh orang barat menjadi Algorism.
Penemu adalah seorang ahli matematika dari uzbeskitan yang bernama Abu Abdullah Muhammad Ibnu Musa Al-Khwarizmi.
Diliteratur barat, beliau lebih terkenal dangan sebutan Algorism. Panggilan inilah yang kemudian dipakai untuk menyebut konsep algoritma yang ditemukannya.
Abu Abdullah Muhammad Ibnu Musa Al-Khuwarizmi (770-840) lahir di Khawarizm (Kheva), kota di selatan sungai Oxus (sekarang Uzbekistan) tahun 770 M. Kedua orangtuanya kemudian pindah kesebuah tempat diselatan kota Bagdad (Irak), ketika masih kecil.
Sebuah karya yang menggunakan angka india, yang pertama kalinya diterjemahkan dan digunakan di barat berjudul al-jam’ wa’l-tafriq bi hisab al-hind(Addition and Substraction in Indian Arithmetics).
Buku tersebut merupakan karya gemulang dari matematikawan muslim Muhammad ibn Musa Al-Khwarismi(780-850M).
John Napier adalah ahli matematika berkebangsaan Inggris, lahir di Merchiston Castle Eidenburg. Napier menyelesaikan sekolah di perancis pada usia 13 tahun, kemudian ia melanjutkan ke Universitas St. Andrews di Scotland.
Ditahun 1612 M, ia menemukan sebuah sistem yang diberi nama “logaritma” yang berasal dari nama khawarizmi itu. Sekarang temuannya itu, lebih dikenal dengan nama logaritma Napier (Napierian Logarithms).
Napier pernah membuat table yang diukir pada gading yang mirip tulang. Lalu, mereka menamainya dengan tulang Napier (Napier’s Bones).
Ketika buku Napier tentang logaritma diterbitkan pada tahun 1614, hal ini amat mengagumkan para ilmuwan sebagaimana ditemukannya kalkulator di zaman modern.
Dengan bantuan logaritma mereka dapat mengerjakan perkalia dan pembagian yang sulit dengan cara cepat dan mudah untuk pertama kalinya. Napier menghabiskan hidupnya mengutak-atik matematika.
Ia meninggal pada tahun 1617 pada usia 67 tahun da dimakamkan di Edinburgh. (Johanes,dkk: 33).
Baca Juga Artikel yang Mungkin Berhubungan : Vektor Matematika : Pengertian, Rumus, Operasi Vektor, Contoh Soal
Oleh karena melihat bilangan basis yang digunakan dalam logaritma waktu itu kurang menyenagkan, maka Henry Briggs (matematikawan Inggris) membuat table umum logaritma (The Table of Common Logarithms) dengan bilangan basis 10 segera setelah itu.
Rumus Logaritma
ac = b → ª log b = c
Keterangan:
a = basis
b = bilangan dilogaritma
c = hasil logaritma
Sifat Logaritma
| ª log a = 1 |
| ª log 1 = 0 |
| ª log aⁿ = n |
| ª log bⁿ = n • ª log b |
| ª log b • c = ª log b + ª log c |
| ª log b/c = ª log b – ª log c |
| ªˆⁿ log b m = m/n • ª log b |
| ª log b = 1 ÷ b log a |
| ª log b • b log c • c log d = ª log d |
| ª log b = c log b ÷ c log a |
Kegunaan Logaritma
Logaritma sering digunakan untuk memecahkan persamaan yang pangkatnya tidak diketahui. Turunannya mudah dicari dan karena itu logaritma sering digunakan sebagai solusi dari integral. Dalam persamaan bn = x, b dapat dicari dengan pengakaran, n dengan logaritma, dan x dengan fungsi eksponensial.
1. Sains dan Teknik
Dalam sains, terdapat banyak besaran yang umumnya diekspresikan dengan logaritma. Sebabnya, dan contoh-contoh yang lebih lengkap, dapat dilihat di skala logaritmik.
- Negatif dari logaritma berbasis 10 digunakan dalam kimia untuk mengekspresikan konsentrasi ion hidronium (pH). Contohnya, konsentrasi ion hidronium pada air adalah 10−7 pada suhu 25 °C, sehingga pH-nya 7.
- Satuan bel (dengan simbol B) adalah satuan pengukur perbandingan (rasio), seperti perbandingan nilai daya dan tegangan. Kebanyakan digunakan dalam bidang telekomunikasi, elektronik, dan akustik. Salah satu sebab digunakannya logaritma adalah karena telinga manusia mempersepsikan suara yang terdengar secara logaritmik. Satuan Bel dinamakan untuk mengenang jasa Alexander Graham Bell, seorang penemu di bidang telekomunikasi. Satuan desibel (dB), yang sama dengan 0.1 bel, lebih sering digunakan.
- Skala Richter mengukur intensitas gempa bumi dengan menggunakan skala logaritma berbasis 10.
- Dalam astronomi, magnitudo yang mengukur terangnya bintang menggunakan skala logaritmik, karena mata manusia mempersepsikan terang secara logaritmik.
Baca Juga Artikel yang Mungkin Berhubungan : Rumus Kuartil, Desil, Persentil LENGKAP
2. Penghitungan yang lebih mudah
Logaritma memindahkan fokus penghitungan dari bilangan normal ke pangkat-pangkat (eksponen). Bila basis logaritmanya sama, maka beberapa jenis penghitungan menjadi lebih mudah menggunakan logaritma::
Sifat-sifat di atas membuat penghitungan dengan eksponen menjadi lebih mudah, dan penggunaan logaritma sangat penting, terutama sebelum tersedianya kalkulator sebagai hasil perkembangan teknologi modern.
Untuk mengkali dua angka, yang diperlukan adalah melihat logaritma masing-masing angka dalam tabel, menjumlahkannya, dan melihat antilog jumlah tersebut dalam tabel.
Untuk mengitung pangkat atau akar dari sebuah bilangan, logaritma bilangan tersebut dapat dilihat di tabel, lalu hanya mengkali atau membagi dengan radix pangkat atau akar tersebut.
Kalkulus
Turunan fungsi logaritma adalah
dimana ln adalah logaritma natural, yaitu logaritma yang berbasis e. Jika b = e, maka rumus di atas dapat disederhanakan menjadi
Integral fungsi logaritma adalah
Integral logaritma berbasis e adalah
Sebagai contoh carilah turunan
Penghitungan Nilai Logaritma
Nilai logaritma dengan basis b dapat dihitung dengan rumus dibawah ini.
Sedangkan untuk logaritma berbasis e dan berbasis 2, terdapat prosedur-prosedur yang umum, yang hanya menggunakan penjumlahan, pengurangan, pengkalian, dan pembagian.
Persamaan Logaritma
Persamaan logaritma adalah persamaan yang peubahnya terdapat dalam bilangan pokok atau numerusnya.
Contoh : (i) log (3x – 1) = log (x – 15) , (ii) (x-1)log 16 = 2, dll Macam-macam bentuk persamaan logaritma :
- alog f(x) = alog p f(x)log a = g(x)log a
- alog f(x) = alog g(x) f(x)log g(x) = f(x)log h(x)
- alog f(x) = blog f(x) A.(a log x)2 + B(a log x) + C = 0
- f(x)log g(x) = p untuk A ¹ 0
Baca Juga Artikel yang Mungkin Berhubungan : Makalah Tentang Aritmatika
Bentuk persamaan logaritma pada umumnya belum sederhana. Untuk menyeder- hanakan persamaan logaritma perlu memperhatikan sifat-sifat logaritma berikut :
Dalam menyelesaikan persamaan logaritma, bilangan pokok logaritma perlu disamakan dahulu. Nilai penyelesaian yang diperoleh perlu diuji dengan mensubstitusikan ke persamaan semula. Nilai penyelesaian yang menjadi anggota himpunan penyelesaian (HP) adalah yang mengakibatkan :
- numerus pada persamaan semula bernilai
- bilangan pokok logaritma pada persamaan semula bernilai positif dan tidak sama dengan 1 (satu).
Contoh soal
Tentukan himpunan penyelesaian dari 2log (2x+1) = 3 !
Jawab:
Fungsi Logaritma
Fungsi Logaritma adalah suatu fungsi invers (balikan) dari fungsi eksponen. Bila fungsi eksponen dinyatakan dengan f(x) = ax, a > 0, a ≠ 1, maka invers dari f(x0 ditulis dengan f-1(x) = alog x atau f(x) = alog x, a > 0, a ≠ 1.
Baca Juga Artikel yang Mungkin Berhubungan : √ 54 Gambar Jaring jaring Balok Lengkap Dengan Contohnya
Secara umum bila y = ax, maka x = alog y.
- Bila f(x) = alog x, dengan a > 1, x > 0 , x e R, maka f(x) dikatakan fungsi
- Bila f(x) = alog x, dengan 0 < a < 1, x > 0 , x e R, maka f(x) dikatakan fungsi naik.
Grafik fungsi logaritma selalu melalui titik (1,0) dan selalu berada di sebelah kanan sumbu Y. Perhatikan gambar di bawah ini:
Pertidaksamaan Logaritma
Dari grafik fungsi logaritma di atas tampak bahwa :
Untuk a > 1
- Bila alog f(x) ³ alog g(x), maka f(x) ³ g(x), dengan syarat f(x) dan g(x) >
- Bila alog f(x) £ alog g(x), maka f(x) £ g(x), dengan syarat f(x) dan g(x) >
Contoh soal :
Tentukan nilai x yang memenuhi pertidaksamaan 2log (2x-3) > 2log 5 !
Penyelesaian:
Kesimpulan : Nilai x yang menjadi penyelesaian pertidaksamaan harus memenuhi (1) dan (2) Jadi nilai x yang memenuhi adalah x > 4.
Baca Juga Artikel yang Mungkin Berhubungan : Rumus Volume Tabung : Luas Permukaan, Tinggi, & Contoh Soal
Contoh Soal dan Penyelesaiannya
1. Nilai dari 2log 4 + 2log 12 – 2log 6 =…
- 8
- 6
- 5
- 4
- 3
Pembahasan :
Untuk soal seperti di atas, maka kita perlu mengingat sifat logaritma
alog(b.c) = alog b + alog c, dan
alog = alog b – alog c
sehingga, untuk menyelesaikan soal di atas, kita gunakan kedua sifat logaritma tersebut. Dimana perhitungannya akan menjadi :
2log 4 + 2log 12 – 2log 6 = 2log
= 2log 8
Kemudian, untuk penyelesaian akhir, kita perlu mengingat sifat berikutnya, yaitu :
alog = n . alog b
→ 8 =
sehingga, penyelesaian akhirnya akan menjadi seperti berikut ini :
2log 8 = 2log
= 3 . 2log 2 → jangan lupa dengan yang ini : alog a = 1
= 3 . 1
= 3 ( E )
2. Nilai dari 2log 48 + 5log 50 – 2log 3 – 5log 2 =…
- -2
- -6
- 2
- 6
Pembahasan :
Sebelum mengerjakan, mari kita lihat perbedaan antara soal no. 1 dengan no. 2. Perbedaannya adalah :
- Pada soal no. 1, indeks logaritma merupakan indeks yang seragam ( indeks 2 )
- Sedangkan pada soal no. 2, indeks logaritma yang digunakan indeks tidak seragam ( indeks 2 dan indeks 5 )
Nah, tentu saja dengan perbedaan seperti ini, maka kita tidak bisa langsung menyelesaikannya seperti soal no. 1 di atas. Akan tetapi, soal no. 2 ini perlu di utak-atik sedikit supaya bisa diselesaikan dengan sifat-sifat yang ada.
Utak-atik yang perlu kita lakukan adalah dengan menggabungkan masing-masing logaritma dengan yang sejenis atau ber-indeks sama ( indeks 2 dengan indeks 2, indeks 5 dengan indeks 5 ), sehingga soal tersebut akan menjadi :
2log 48 – 2log 3 + 5log 50 – 5log 2 =…
Kemudian, soal tersebut bisa kita hitung dengan sifat :
alog = alog b – alog c
2log 48 – 2log 3 + 5log 50 – 5log 2 = 2log + 5log
= 2log 16 + 5log 25
Sekarang kita gunakan sifat berikutnya : alog = n . alog b
→ 16 =
→ 25 =
Dan juga gunakan sifat : alog a = 1
Sehingga, penyelesaiannya akan menjadi :
2log + 5log = 4 . 2log + 2 . 5log
= 4 + 2
= 6 ( E )
3. Jika log 3 = 0,4771 dan log 2 = 0,3010, maka nilai dari log 75 =…
- 0,7781
- 0,9209
- 1,0791
- 1,2552
- 1,8751
Pembahasan :
Untuk soal yang modelnya begini ini, ada kunci pengerjaannya yang harus kita paham. Yaitu adalah keterangan yang menunjukkan nilai log 2 dan log 3. Dengan adanya keterangan tambahan tersebut, berarti yang harus ada di pikiran kita adalah bagaimana mengubah bentuk log 75 menjadi bentuk logaritma yang mengandung unsur bilangan 2 dan 3.
→ 75 = 3 . 25 = 3 .
Sehingga, bila kita ubah bilangan 75 tersebut dengan 3. , maka akan kita dapatkan :
log 75 = log ( 3 . ) → dengan ini, kita harus ingat sifat : alog(b.c) = alog b + alog c
= log 3 + log → jangan lupa bahwa : alog = n . alog b
= log 3 + 2 . log 5
Maksudnya adalah dengan mengubah bilangan 5 pada log 5 tersebut, karena di dalam soal yang diberi keterangan adalah log 2 dan log 3, sedangkan log 5 tidak diberi keterangan apapun.
Untuk itu, trik yang perlu dilakukan di sini adalah :
→ 5 =
Bilangan 5 tersebut perlu kita ubah ke dalam suatu bilangan yang mengandung unsur bilangan 2 dan nilainya tidak berubah ( tetap bernilai 5 ). Sehingga, jika kita selesaikan, akan menjadi :
log 75 = log 3 + 2 . log → tentu masih ingat sifat alog = alog b – alog c, kan?
= log 3 + 2 ( log 10 – log 2 ) → log 10 = 10log 10 = 1 → alog a = 1
= 0,4771 + 2 ( 1 – 0,3010 )
= 1,8751 ( E )
4. Diketahui 2log 3 = 1,6 dan 2log 5 = 2,3; nilai dari 2log ..
- 10,1
- 6,9
- 5,4
- 3,2
- 3,7
Pembahasan :
Sedikit mirip dengan soal sebelumnya, dengan mengetahui ada keterangan di dalam soal mengenai nilai dari sebuah logaritma suatu bilangan, maka yang perlu kita lakukan adalah dengan mengubahnya ke dalam bentuk yang mengandung unsur bilangan yang sesuai dengan keterangan tersebut.
→ 125 = 5 . 5 . 5 =
→ 9 =
Sehingga, jika kita selesaikan soal tersebut, akan menjadi :
2log = 2log → bisa ditebak kan? Di sini kita perlu sifat : alog = alog b – alog c
= 2log – 2log
Kemudian, sifat logaritma yang kita gunakan berikutnya adalah sifat :
alog = n . alog b
maka, persamaan di atas selanjutnya akan menjadi :
= 3 . 2log 5 – 2 . 2log 3
= 3 . ( 2,3 ) – 2. ( 1,6 )
= 6,9 – 3,2
= 3,7 ( E )
5. Nilai dari 2log 8 – 1/2log 0,25 + 3log + 2log 1 =…
- -2
- -1
- 0
- 1
- 2
Pembahasan :
Pada soal kali ini, masih mirip dengan soal-soal sebelumnya. Yaitu, penyederhanaan logaritma dengan cara menggabungkan beberapa fungsi log yang memiliki indeks sama.
Jadi, untuk menggabungkan fungsi log tersebut kita harus tahu mana yang memiliki indeks yang sama.
Yang memiliki indeks yang sama adalah 2log 8; 1/2log 0,25; 2log 1
Dari ketiga fungsi log di atas, ada satu yang diwarnai merah, yaitu 1/2log 0,25 karena fungsi yang ini perlu kita ubah sedikit supaya menjadi indeks 2. Jadi, yang perlu kita lakukan adalah dengan menggunakan salah satu sifat logaritma, yaitu sifat :
Sehingga, bentuk 1/2log 0,25 bisa kita ubah menjadi
Setelah kita dapatkan bentuk sebelumnya menjadi ber-indeks 2, maka sekarang kita bisa mulai menyelesaikan soal di atas dengan menggunakan sifat-sifat dasar seperti soal sebelumnya, yaitu:
alog(b.c) = alog b + alog c, dan
alog = alog b – alog c
Sehingga, pengerjaannya akan menjadi :
2log 8 – 1/2log 0,25 + 3log + 2log 1 = 2log 8 – 2log 4 + 3log + 2log 1
= 2log + 3log
Ingat! Bahwa : =
2log 8 – 1/2log 0,25 + 3log + 2log 1 = 2log 2 + 3log → alog = n . alog b
= 1 + ( -3 )
= -2 ( A )
Itulah ulasan tentang Logaritma : Rumus, Sifat, Fungsi, Persamaan dan Contoh Soal. Semoga apa yang diulas diatas bermanfaat bagi pembaca setia GuruPendidikan. Sekian dan Terima kasih.