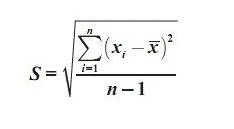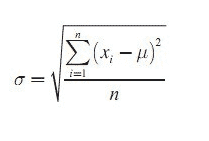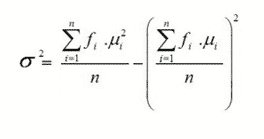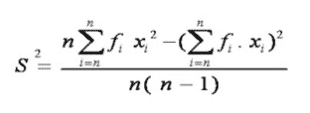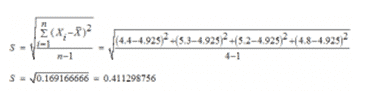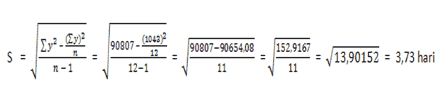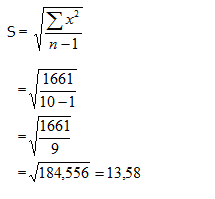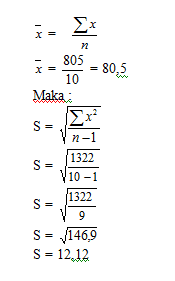Standar deviasi disebut juga simpangan baku. Seperti halnya varians, standar deviasi juga merupakan suatu ukuran dispersi atau variasi. Standar deviasi merupakan ukuran dispersi yang paling banyak dipakai. Hal ini mungkin karena standar deviasi mempunyai satuan ukuran yang sama dengan satuan ukuran data asalnya. Misalnya, bila satuan data asalnya adalah cm, maka satuan stdar deviasinya juga cm. Sebaliknya, varians memiliki satuan kuadrat dari data asalnya (misalnya cm2). Simbol standar deviasi untuk populasi adalah σ dan untuk sampel adalah s.
Baca Juga Artikel yang Mungkin Berhubungan : Logaritma : Rumus, Sifat, Fungsi, Persamaan dan Contoh Soal
Pengertian Standar Deviasi
Standar deviasi adalah ukuran penyebaran yang paling banyak digunakan. Semua gugus data dipertimbangkan sehingga lebih stabil dibandingkan dengan ukuran lainnya. Namun, apabila dalam gugus data tersebut terdapat nilai ekstrem, standar deviasi menjadi tidak sensitif lagi, samahalnya seperti mean.
Rumus Standar Deviasi
Berikut terdapat empat (4) rumus dalam standar deviasi, diantaranya:
-
1. Rumus Standar Deviasi Data Tunggal
-
2. Rumus Standar Deviasi Data Populasi
-
3. Rumus Standar Deviasi Data Kelompok untuk Sampel
-
4. Rumus Standar Deviasi Data Kelompok untuk Populasi
Keterangan:
- σ2 = variansatauragamuntukpopulasi
- S2 = variansatauragamuntuksampel
- fi = Frekuensi
- xi = Titiktengah
- x¯ = Rata-rata (mean) sampeldan μ = rata-rata populasi
- n = Jumlah data
Baca Juga Artikel yang Mungkin Berhubungan : 17 Pengertian Matematika Menurut Para Ahli Beserta Bidangnya
Cara Menghitung Standar Deviasi
Berikut terdapat tiga (3) cara menghitung dalam standar deviasi, diantaranya:
-
1. Cara Menghitung Standar Deviasi Data Tunggal
Langkah 1:
Cari dulu nilai rata-ratanya
X̄ = ΣX : n = 4.4+5.3+5.2+4.8 : 4 = 4.925
Langkah 2:
Cari standar deviasi tunggal
-
2. Cara Menghitung Standar Deviasi Data Populasi
Langkah 1:
Cari dulu nilai rata-ratanya
X̄= 4.925
Langkah 2:
Cari standar deviasi populasi
-
3. Cara Menghitung Standar Deviasi Mengunakan Excel
Langkah 1:
Buat tabel seperti dibawah
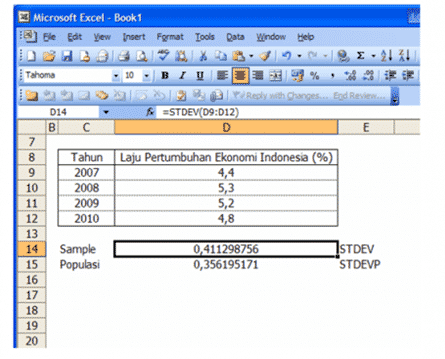
Langkah 2:
Masukan formulasi “=STDEV(number1;[number2];….[number4])” untuk data sample, dan “=STDEVP(number1;[number2];….[number4])” untuk data populasi.
Baca Juga Artikel yang Mungkin Berhubungan : Vektor Matematika : Pengertian, Rumus, Operasi Vektor, Contoh Soal
Perhatikan bagan dibawah ini :
Bagi Sobat yang mencari aplikasi bermanfaat, kami sarankan untuk mencoba mengakses situs technicaltalk.net untuk download aplikasi sepuasnya secara gratis di sana.
Contoh Standar Deviasi
Berikut ini terdapat beberapa contoh dari standar deviasi, diantaranya:
1. Data umur berbunga (hari) tanaman padi varietas Pandan Wangi adalah sbb: 84 86 89 92 82 86 89 92 80 86 87 90
Berapakah standar deviasi dari data di atas?
|
Sampel |
y |
y2 |
|
1 |
84 |
7056 |
|
2 |
86 |
7396 |
|
3 |
89 |
7921 |
|
4 |
92 |
8464 |
|
5 |
82 |
6724 |
|
6 |
86 |
7396 |
|
7 |
89 |
7921 |
|
8 |
92 |
8464 |
|
9 |
80 |
6400 |
|
10 |
86 |
7396 |
|
11 |
87 |
7569 |
|
12 |
90 |
8100 |
|
Jumlah |
1043 |
90807 |
Maka nilai standar deviasi data di atas adalah
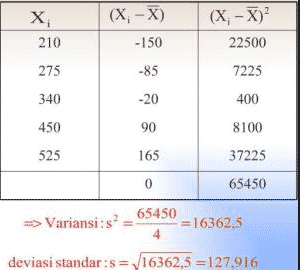
2. Jika dimiliki data : 210, 340, 525, 450, 275
maka variansi dan standar deviasinya :
mean = (210, 340, 525, 450, 275)/5 = 360
variansi dan standar deviasi berturut-turut :
Sedangkan jika data disajikan dalam tabel distribusi frekuensi, variansi sampel dapat dihitung sebagai :
Baca Juga Artikel yang Mungkin Berhubungan : Rumus Kuartil, Desil, Persentil LENGKAP
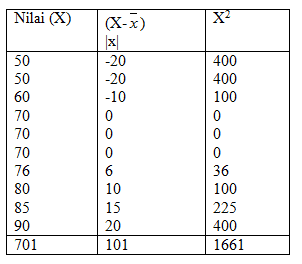
3. Data nilai UTS yang diambil sampel 10 orang:
Kelas A : 50, 50, 60, 70, 70, 70, 76, 80, 85, 90
Jawaban:
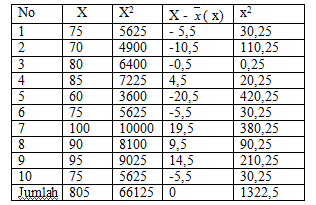
4. Dari hasil survai yang melihat bagaimana kepemimpinan 10 orang mahasiswa yang aktif dalam organisasi intra kampus. Data berikut memperlihatkan nilai kepemimpinan 10 orang responden tersebut.
Jawaban:
Jadi dapat disimpulkan bahwa rata-rata nilai kepemimpinan mahasiswa yang aktif dalam organisasi intra kampus adalah 80, 5 dengan standar deviasi (penyimpangan) 12,12.
Baca Juga Artikel yang Mungkin Berhubungan : Makalah Tentang Aritmatika
5. Laju pertumbuhan ekonomi Indonesia (dinyatakan dalam persentase) dalam kurun waktu 2007 sampai dengan 2010 adalah sebagai berikut : 4.4, 5.3, 5.2 dan 4.8.
Hitunglah standar deviasi sample dan populasinya dengan menggunakan rumus baku dan formulasi Excel.
Jawaban:
Itulah Materi Lengkapnya Semoga apa yang diulas diatas bermanfaat bagi pembaca setia GuruPendidikan. Sekian dan Terima kasih.