Hukum gerak Newton adalah hukum sains yang ditentukan oleh Sir Isaac Newton mengenai sifat gerak benda. Hukum gerak Newton itu sendiri merupakan hukum yang fundamental. Artinya, pertama hukum ini tidak dapat dibuktikan dari prinsip-prinsip lain, kedua hukum ini memungkinkan kita agar dapat memahami jenis gerak yang paling umum yang merupakan dasar mekanika klasik.
Dalam kehidupan sehari-hari, gaya merupakan tarikan atau dorongan. Misalnya, pada waktu kita mendorong atau menarik suatu benda atau kita menendang bola, dikatakan bahwa kita mengerjakan suatu gaya dorong pada mobil mainan. Pada umumnya benda yang dikenakan gaya mengalami perubahan-perubahan lokasi atau berpindah tempat.
Pengertian Hukum Newton
Hukum Newton adalah hukum yang mengatur tentang gerak. Hukum gerak Newton itu sendiri merupakan hukum yang fundamental. Artinya, pertama hukum ini tidak dapat dibuktikan dari prinsip-prinsip lain. Kedua, hukum ini memungkinkan kita agar dapat memahami jenis gerak yang paling umum yang merupakan dasar mekanika klasik.
Hukum gerak Newton adalah tiga hukum yang menjadi dasar mekanika klasik. Hukum ini menggambarkan hubungan antara gaya yang bekerja pada suatu benda dan gerak yang disebabkannya. Ketiga hukum gerak ini pertama dirangkum oleh Isaac Newton dalam karyanya Philosophi Naturalis Principa Mathematica, pertama kali ditebitkan pada 05 Juli 1687.
Baca Juga Artikel Yang Mungkin Berhubungan : Hukum Kepler 1 2 3
Bunyi Hukum Newton 1
“Jika resultan dari gaya-gaya yang bekerja pada benda sama dengan nol maka benda diam akan tetap diam dan benda bergerak lurus beraturan akan tetap bergerak lurus beraturan“.
Hukun Newton Pertama Sebagai Hukum Kelembaman
Hukum pertama Newton menyatakan bahwa sebuah benda dalam keadaan diam atau bergerak dengan kecepatan konstan akan tetap diam atau akan terus bergerak dengan kecepatan konstan kecuali ada gaya eksternal yang bekerja pada benda itu. Kecenderungan ini digambarkan dengan mengatakan bahwa benda mempunyai kelembaman.
Benda yang mula-mula diam akan mempertahankan keadaan diamnya (malas bergerak), dan benda yang mula-mula bergerak akan mempertahankan keadaan bergeraknya (malas berhenti). Sifat benda yang cenderung mempertahankan keadaan geraknya (diam atau bergerak) inilah yang disebut kelembaman atau inersia (kemalasan). Oleh karena itu hukum pertama Newton disebut juga hukum Kelembaman atau Hukum inersia.
Baca Juga Artikel Yang Mungkin Berhubungan : Hukum Ohm
Contoh hukum Newton 1 :
- Sediakan alat-alat antara lain Kelereng, kertas, dan meja!
- Letakkan kelereng di atas kertas pada meja yang mendatar hingga keadaan kelereng diam!
- Tarik kertas dengan mendadak / sentakan!
- Ulangi langkah (ii) tetapi kertas ditarik perlahan-lahan, kemudian hentikan kertas tersebut secara mendadak!
- Amati yang terjadi!
Berdasarkan kegiatan diatas, dapat disimpulkan bahwa setiap benda yang diam cenderung untuk tetap diam dan benda yang bergerak lurus beraturan cenderung untuk tetap bergerak lurus beraturan (ingin mempertahankan keadaannya). Sifat demikian itulah yang disebut sebagai kelembaman (inersia) suatu benda.
Hukum Newton dapat dinyatakan dalam bentuk persamaan F = 0
Baca Juga Artikel Yang Mungkin Berhubungan : Hukum Hooke
Bunyi Hukum Newton 2
“Percepatan yang ditimbulkan oleh gaya yang bekerja pada suatu benda berbanding lurus dengan besar gaya itu ( searah dengan gaya itu ) dan berbanding terbalik dengan massa benda tersebut”.
Secara matematis dapat ditulis :
a =
Dimana :
F = gaya, Satuannya N
m = massa, Satuannya Kg
a = Percepatan, Satuannya ms-2
Gaya, Massa, dan Hukum Kedua Newton
Hukum kedua Newton menetapkan hubungan antara besaran dinamika gaya dan massa dan besaran kinematika percepatan, kecepatan, dan perpindahan. Gaya adalah suatu pengaruh pada sebuah benda yang menyebabkan benda mengubah kecepatannya, artinya dipercepat. Arah gaya adalah arah percepatan yang disebabkan jika gaya itu adalah satu-satunya gaya yang bekerja pada benda tersebut. Besarnya gaya adalah hasil kali massa benda dan besarnya percepatan yang dihasilkan gaya. Massa adalah sifat intristik sebuah benda mengukur resistensinya terhadap percepatan.
Contoh Hukum 2 Newton :
Pada gambar disamping, sebuah benda ditarik dengan gaya F. Dengan adanya gaya F, maka benda bergerak dengan percepatan a. Pada kasus yang kedua, benda dengan massa m ditarik oleh 2 orang dengan gaya 2F. Pada Kasus yang kedua ini, benda bergerak dengan percepatan 2a, massa benda ditambah dan ditarik dengan gaya F. Pada kasus yang ketiga benda bergerak dengan percepatana/2 .
Dalam hukum ini, Newton menyimpulkan sebagai berikut :
- Percepatan benda yang disebabkan adanya resultan gaya pada benda dengan massa m berbanding langsung ( sebanding ) dengan besar resultan gaya. Makin besar gaya, makin besar percepatan.
- Percepatan benda yang disebabkan adanya resultan gaya pada benda berbanding terbalik dengan massa benda m. Makin besar massa, makin kecil percepatan.
Contoh soal :
Mobil-mobilan bermassa 2 Kg diam diatas lantai licin, kemudian diberi gaya tertentu dan bergerak dengan percepatan 10m/s2. Berapakah gaya yang diberikan pada mobil-mobilan?
Diketahui : m = 2 Kg
a = 10 m/s2
Ditanya : F ?
Jawab : F = m.a
= 2 Kg . 10 m/s2 = 20 N
Baca Juga Artikel Yang Mungkin Berhubungan : Hukum Archimedes
Bunyi Hukum Newton 3
Hukum III Newton tentang gerak menyatakan bahwa bila suatu benda melakukan gaya pada benda lainnya, maka akan menimbulkan gaya yang besarnya sama dengan arah yang berlawanan. Dengan kata lain, Hukum III Newton ini berbunyi :
Gaya aksi = gaya reaksi.
Gaya aksi = gaya yang bekerja pada benda.
Gaya reaksi = gaya reaksi benda akibat gaya aksi.
Untuk setiap gaya aksi yang dilakukan, selalu ada gaya reaksi yang besarnya sama tetapi arahnya berlawanan, atau gaya interaksi antara dua buah benda selalu sama besar tetapi berlawanan arah. Harus selalu diingat bahwa pasangan gaya yang dimaksudkan dalam Hukum III Newton ini bekerja pada dua benda yang berbeda.
Gaya mana yang merupakan gaya reaksi pada dasarnya tidak dapat ditentukan. Namun demikian, biasanya dalam soal fisika disebutkan bahwa gaya aksi adalah gaya yang kita lakukan, meskipun sebenarnya bisa dipertukarkan.
Hukum ketiga menyatakan bahwa tidak ada gaya timbul di alam semesta ini, tanpa keberadaan gaya lain yang sama dan berlawanan dengan gaya itu. Jika sebuah gaya bekerja pada sebuah benda ( aksi ) maka benda itu akan mengerjakan gaya yang sama besar namun berlawanan arah ( reaksi ).
Dengan kata lain gaya selalu muncul berpasangan. Tidak pernah ada gaya yang muncul sendirian.
Sebagai Contoh, ketika kita berjalan, telapak kaki kita mendorong tanah kebelakang ( aksi ). Sebagai reaksi, tanah mendorong telapak kaki kita ke depan, sehingga kita berjalan kedepan.
Contoh lain, Ketika seseorang mendayung perahu, pada waktu mengayunkan dayung, pendayung mendorong air ke belakang ( aksi ). Sebagai reaksi, air memberi gaya pada dayung kedepan sehingga perahu bergerak kedepan.
Secara matematis, Hukum III Newton ditulis sebagai berikut :
| FA = – FB | Atau | Faksi = – Freaksi |
Yang bisa dibaca sebagai “ gaya benda A yang bekerja pada benda B sama dengan negativ gaya benda B yang bekerja pada benda A ”
Contoh Soal Dan Pembahasan Hukum Newton
Soal No. 1
Perhatikan gambar berikut!

Benda bermassa m = 10 kg berada di atas lantai kasar ditarik oleh gaya F = 12 N ke arah kanan. Jika koefisien gesekan statis antara benda dan lantai adalah 0,2 dengan koefisien gesekan kinetis 0,1 tentukan besarnya :
a) Gaya normal
b) Gaya gesek antara benda dan lantai
c) Percepatan gerak benda
Pembahasan
Gaya-gaya pada benda diperlihatkan gambar berikut:

a) Gaya normal
Σ Fy = 0
N − W = 0
N − mg = 0
N − (10)(10) = 0
N = 100 N
b) Gaya gesek antara benda dan lantai
Cek terlebih dahulu gaya gesek statis maksimum yang bisa terjadi antara benda dan lantai:
fsmaks = μs N
fsmaks = (0,2)(100) = 20 N
Ternyata gaya gesek statis maksimum masih lebih besar dari gaya yang menarik benda (F) sehingga benda masih berada dalam keadaan diam. Sesuai dengan hukum Newton untuk benda diam :
Σ Fx = 0
F − fges = 0
12 − fges = 0
fges = 12 N
c) Percepatan gerak benda
Benda dalam keadaan diam, percepatan benda NOL
Soal No. 2
Perhatikan gambar berikut, benda mula-mula dalam kondisi rehat!

Benda bermassa m = 10 kg berada di atas lantai kasar ditarik oleh gaya F = 25 N ke arah kanan. Jika koefisien gesekan statis antara benda dan lantai adalah 0,2 dengan koefisien gesekan kinetis 0,1 tentukan besarnya :
a) Gaya normal
b) Gaya gesek antara benda dan lantai
c) Percepatan gerak benda
d) Jarak yang ditempuh benda setelah 2 sekon
Pembahasan
Gaya-gaya pada benda diperlihatkan gambar berikut:

a) Gaya normal
Σ Fy = 0
N − W = 0
N − mg = 0
N − (10)(10) = 0
N = 100 N
b) Gaya gesek antara benda dan lantai
Cek terlebih dahulu gaya gesek statis maksimum yang bisa terjadi antara benda dan lantai:
fsmaks = μs N
fsmaks = (0,2)(100) = 20 N
Ternyata gaya yang gesek statis maksimum (20 N) lebih kecil dari gaya yang menarik benda (25 N), Sehingga benda bergerak. Untuk benda yang bergerak gaya geseknya adalah gaya gesek dengan koefisien gesek kinetis :
fges = fk = μk N
fges = (0,1)(100) = 10 N
c) Percepatan gerak benda
Hukum Newton II :
Σ Fx = ma
F − fges = ma
25 − 10 = 10a
a = 15/10 = 1,5 m/s2
d) Jarak yang ditempuh benda setelah 2 sekon
S = Vo t + 1/2 at2
S = 0 + 1/2(1,5)(22)
S = 3 meter
Soal No. 3
Perhatikan gambar berikut, benda 5 kg mula-mula dalam kondisi tidak bergerak!

Jika sudut yang terbentuk antara gaya F = 25 N dengan garis mendatar adalah 37o, koefisien gesek kinetis permukaan lantai adalah 0,1 dan percepatan gravitasi bumi 10 m/s2 tentukan nilai:
a) Gaya normal
b) Gaya gesek
c) Percepatan gerak benda
(sin 37o = 0,6 dan cos 37o = 0,8)
Pembahasan
Gaya-gaya pada benda diperlihatkan gambar berikut:

a) Gaya normal
Σ Fy = 0
N + F sin θ − W = 0
N = W − F sin θ = (5)(10) − (25)(0,6) = 35 N
b) Gaya gesek
Jika dalam soal hanya diketahui koefisien gesek kinetis, maka dipastikan benda bisa bergerak, sehingga fges = fk :
fges = μk N
fges = (0,1)(35) = 3,5 N
c) Percepatan gerak benda
Σ Fx = ma
F cos θ − fges = ma
(25)(0,8) − 3,5 = 5a
5a = 16,5
a = 3,3 m/s2
Soal No. 4
Perhatikan gambar berikut, balok 100 kg diluncurkan dari sebuah bukit!

Anggap lereng bukit rata dan memiliki koefisien gesek 0,125. Percepatan gravitasi bumi 10 m/s2 dan sin 53o = 0,8, cos 53o = 0,6. Tentukan nilai dari :
a) Gaya normal pada balok
b) Gaya gesek antara lereng dan balok
c) Percepatan gerak balok
Pembahasan
Gaya-gaya pada balok diperlihatkan gambar berikut:
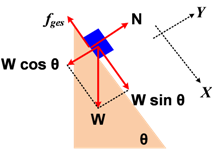
a) Gaya normal pada balok
Σ Fy = 0
N − W cos θ = 0
N − mg cos 53o = 0
N − (100)(10)(0,6) = 0
N = 600 Newton
b) Gaya gesek antara lereng dan balok
fges = μk N
fges = (0,125)(600) = 75 newton
c) Percepatan gerak balok
Σ Fx = ma
W sin θ − fges = ma
mg sin 53o − fges = ma
(100)(10)(0,8) − 75 = 100a
a = 725/100 = 7,25 m/s2
Soal No. 5
Balok A massa 40 kg dan balok B massa 20 kg berada di atas permukaan licin didorong oleh gaya F sebesar 120 N seperti diperlihatkan gambar berikut!

Tentukan :
a) Percepatan gerak kedua balok
b) Gaya kontak yang terjadi antara balok A dan B
Pembahasan
a) Percepatan gerak kedua balok
Tinjau sistem :
Σ F = ma
120 = (40 + 20) a
a = 120/60 m/s2
b) Gaya kontak yang terjadi antara balok A dan B
Cara pertama, Tinjau benda A :

Σ F = ma
F − Fkontak = mA a
120 − Fkontak = 40(2)
Fkontak = 120 − 80 = 40 Newton
Cara kedua, Tinjau benda B :

Σ F = ma
Fkontak = mB a
Fkontak = 20(2) = 40 Newton
Soal No. 6
Balok A dan B terletak pada permukaan bidang miring licin didorong oleh gaya F sebesar 480 N seperti terlihat pada gambar berikut!
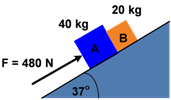
Tentukan :
a) Percepatan gerak kedua balok
b) Gaya kontak antara balok A dan B
Pembahasan
a) Percepatan gerak kedua balok
Tinjau Sistem :
Gaya-gaya pada kedua benda (disatukan A dan B) terlihat pada gambar berikut:
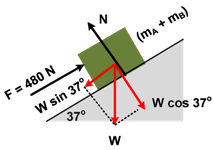
Σ F = ma
F − W sin 37o = ma
480 − (40 + 20)(10)(0,6) = (40 + 20) a
a = 120/60 = 2 m/s2
b) Gaya kontak antara balok A dan B
Cara pertama, tinjau balok A
Gaya-gaya pada balok A terlihat pada gambar berikut :

Σ F = ma
F − WA sin 37o − Fkontak = mA a
480 − (40)(10) (0,6) − Fkontak = (40)(2)
480 − 240 − 80 = Fkontak
Fkontak = 160 Newton
Cara kedua, tinjau benda B
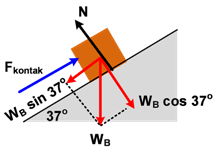
Σ F = ma
Fkontak − WB sin 37o = mB a
Fkontak − (20)(10)(0,6) =(20)(2)
Fkontak = 40 + 120 = 160 Newton
Soal No. 7

Balok A beratnya 100 N diikat dengan tali mendatar di C (lihat gambar). Balok B beratnya 500 N. Koefisien gesekan antara A dan B = 0,2 dan koefisien gesekan antara B dan lantai = 0,5. Besarnya gaya F minimal untuk menggeser balok B adalah….newton
A. 950
B. 750
C. 600
D. 320
E. 100
(Sumber Soal : UMPTN 1993)
Pembahasan
fAB → gaya gesek antara balok A dan B
fBL → gaya gesek antara balok B dan lantai
fAB = μAB N
fAB = (0,2)(100) = 20 N
fBL = μBL N
fBL = (0,5)(100 + 500) = 300 N
Tinjau benda B

Σ Fx = 0
F − fAB − fBL = 0
F − 20 − 300 = 0
F = 320 Newton
Soal No. 8
Benda pertama dengan massa m1 = 6 kg dan benda kedua dengan massa m2 = 4 kg dihubungkan dengan katrol licin terlihat pada gambar berikut !

Jika lantai licin dan m2 ditarik gaya ke kanan F = 42 Newton, tentukan :
a) Percepatan benda pertama
b) Percepatan benda kedua
c) Tegangan tali T
Pembahasan
a) Percepatan benda pertama
Hubungan antara percepatan benda pertama (a1) dan percepatan benda kedua (a2) adalah:
a1 = 2a2
atau
a2 = 1/2a1
Tinjau m2

F − 2T = m2a2
42 − 2T = 4a2
42 − 2T = 4(1/2)a1
42 − 2T = 2a1 (Pers. 1)
Tinjau m1

T = m1a1
T = 6 a1 (Pers. 2)
Gabung Pers. 1 dan Pers. 2
42 − 2T = 2a1
42 − 2(6a1) = 2a1
42 = 14 a1
a1 = 42/14 = 3 m/s2
b) Percepatan benda kedua
a2 = 1/2a1
a2 = 1/2(3) = 1,5 m/s2
c) Tegangan tali T
T = 6a1 = 6(3) = 18 Newton
Soal No. 9
Massa A = 4 kg, massa B = 6 kg dihubungkan dengan tali dan ditarik gaya F = 40 N ke kanan dengan sudut 37o terhadap arah horizontal!

Jika koefisien gesekan kinetis kedua massa dengan lantai adalah 0,1 tentukan:
a) Percepatan gerak kedua massa
b) Tegangan tali penghubung antara kedua massa
Pembahasan
Tinjauan massa B :
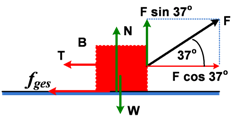
Nilai gaya normal N :
Σ Fy = 0
N + F sin 37o = W
N + (40)(0,6) = (6)(10)
N = 60 − 24 = 36 N
Besar gaya gesek :
fgesB = μk N
fgesB = (0,1)(36) = 3,6 N
Hukum Newton II:
Σ Fx = ma
F cos 37o − fgesB − T = ma
(40)(0,8) − 3,6 − T = 6 a
28,4 − T = 6 a → (persamaan 1)
Tinjauan gaya-gaya pada massa A

Σ Fx = ma
T − fgesA = ma
T − μk N = ma
T − μk mg = ma
T − (0,1)(4)(10) = 4 a
T = 4a + 4 → Persamaan 2
Gabung 1 dan 2
28,4 − T = 6 a
28,4 − ( 4a + 4) = 6 a
24,4 = 10a
a = 2,44 m/s2
b) Tegangan tali penghubung antara kedua massa
T = 4a + 4
T = 4(2,44) + 4
T = 13,76 Newton
Soal No. 10
Diberikan gambar sebagai berikut!
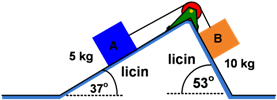
Jika massa katrol diabaikan, tentukan:
a) Percepatan gerak kedua benda
b) Tegangan tali penghubung kedua benda
Pembahasan
Tinjau A

Σ Fx = ma
T − WA sin 37o = mA a
T − (5)(10)(0,6) = 5 a
T − 30 = 5a → (Persamaan 1)
Tinjau B
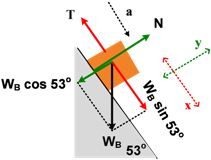
Σ Fx = ma
WB sin 53o − T = mB a
(10)(0,8) − T = 10 a
T = 80 − 10 a → (Persamaan 2)
Gabung 1 dan 2
T − 30 = 5a
(80 − 10 a) − 30 = 5 a
15 a = 50
a = 50/15 = 10/3 m/s2
b) Tegangan tali penghubung kedua benda
T − 30 = 5a
T − 30 = 5( 10/3)
T = 46,67 Newton
