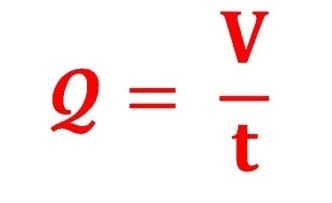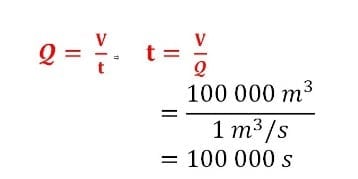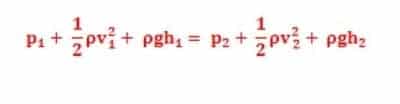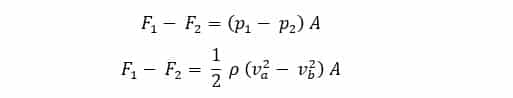Materi Fluida Dinamis : Rumus Hukum Bernoulli, Pengertian, Jenis, Ciri Dan Contoh Soal Tahukah anda apa yang dimaksud Fluida dinamis ??? Jika anda belum mengetahuinya anda tepat sekali mengunjungi gurupendidikan.com. Karena pada kesempatan kali ini disini akan mengulas tentang pengertian Fluida dinamis, jenis aliran Fluida dinamis, ciri Fluida dinamis, dan rumus beserta contoh soalnya secara lengkap oleh karena itu marilah simak ulasan yang ada dibawah berikut ini.
Pengertian Fluida Dinamis
Fluida dinamis adalah fluida (bisa berupa zat cair, gas) yang bergerak. Untuk memudahkan dalam mempelajari, fluida disini dianggap steady (mempunyai kecepatan yang konstan terhadap waktu), tak termampatkan (tidak mengalami perubahan volume), tidak kental, tidak turbulen (tidak mengalami putaran-putaran).
Hidrodinamika merupakan ilmu yang mempelajari tentang fluida bergerak. Sebelum mempelajari fluida bergerak perlu diketahui fluida ideal dan jenis-jenis aliran fluida.
Fluida Ideal
Fluida ideal yaitu fluida yang tidak kompresibel, berpindah tanpa mengalami gesekan, dan aliranya stationer.
- Alirannya tunak (steady), yaitu kecepatan setiap partikel fluida pada satu titik tertentu adalah tetap, baik besar maupun arahnya. Aliran tunak terjadi pada aliran yang pelan.
- Alirannya tak rasional, artinya pada setiap titik partikel fluida tidak memiliki momentum sudut terhadap titik tersebut. Alirannya mengikuti garis arus (streamline).
- Tidak komprisibel (tidak termampatkan), artinya fluida tidak mengalami perubahan volume (massa jenis) karena pengaruh tekanan.
- Tak kental, artinya tidak mengalami gesekan baik dengan lapisan fluida disekitarnya maupun dengan dinding tempat yang dilaluinya. Kekentalan pada aliran fluida berkaitan dengan viskositas.
Jenis Aliran Fluida
Ada beberapa jenis aliran fluida. Lintasan yang ditempuh suatu fluida yang sedang bergerak disebut garis alir. Berikut ini beberapa jenis aliran fluida yaitu sebagai berikut :
- Aliran lurus atau laminer yaitu aliran fluida mulus. Lapisan-lapisan yang bersebelahan meluncur satu sama lain dengan mulus. Pada aliran ini partikel fluida mengikuti lintasan yang mulus dan lintasan ini tidak saling bersilangan. Aliran laminer dijumpai pada air yang dialirkan melalui pipa atau slang.
- Aliran turbulen yaitu aliran yang ditandai dengan adanya lingkaran-lingkaran tak menentu dan menyerupai pusaran. Aliran turbulen sering dijumpai di sungai-sungai dan selokan-selokan.
Ciri-Ciri Fluida Dinamis
Ciri-Ciri umum dari fluida dinamis yaitu sebagai berikut :
- fluid dianggap tidak kompetibel
- fluid dianggap bergerak tanpa gesekan, walaupun ada gerakan materi (tidak mempunyai kekentalan)
- aliran fluida adalah aliran stsioner yaitu kecepatan dan arah gerak partikel pluida yang melalui suatu titik tertentu selalu tetap
- tak bergantung waktu (tunak), artinya kecepatannya konstan pada titik tertentu, dan membentuk aliran leminer (berlapis)
Rumus Fluida Dinamis
Besaran-besaran dalam fluida dinamis
Debit aliran (Q)
Jumlah volume fluida yang mengalir persatuan waktu, atau:
Dimana :
Q = debit aliran (m3/s)
A = luas penampang (m2)
V = laju aliran fluida (m/s)
Aliran fluida sering dinyatakan dalam debit aliran
Dimana :
Q = debit aliran (m3/s)
V = volume (m3)
t = selang waktu (s)
Contoh Soal
Suatu pipa mengalirkan air dengan debit 1m3 tiap sekonnya, dan digunakan untuk mengisi bendungan berukuran ( 100 x 100 x 10 ) m. Hitung waktu yang dibutuhkan untuk mengisi bendungan sampai penuh !
Jawab :
Jadi, Waktu yang dibutuhkan untuk mengisi bendungan sampai penuh yaitu 100.000 s
Persamaan Kontinuitas
Persamaan kontinuitas adalah persamaan yang menghubungkan kecepatan fluida dalam dari satu tempat ke tempat lain. Sebelum menurunkan hubungan, Anda harus memahami beberapa istilah dalam aliran fluida. Garis aliran (stream line) diartikan sebagai jalur aliran fluida ideal (aliran lunak). Garis singgung di suatu titik pada garis memberikan kita arah kecepatan aliran fluida. Garis alir tidak berpotongan satu sama lain. Tabung air adalah kumpulan dari garis-garis aliran.
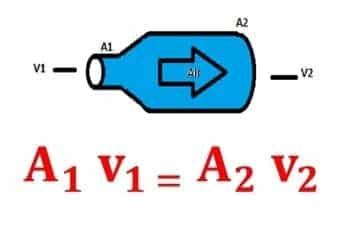
Air yang mengalir di dalam pipa air dianggap mempunyai debit yang sama di sembarang titik. Atau jika ditinjau 2 tempat, maka:
Debit aliran 1 = Debit aliran 2, atau :
Persamaan Hukum Bernoulli
Hukum Bernoulli adalah hukum yang berlandaskan pada hukum kekekalan energi yang dialami oleh aliran fluida. Hukum ini menyatakan bahwa jumlah tekanan (p), energi kinetik per satuan volume, dan energi potensial per satuan volume memiliki nilai yang sama pada setiap titik sepanjang suatu garis arus. Jika dinyatakan dalam persamaan menjadi :
Dimana :
p = tekanan air (Pa)
v = kecepatan air (m/s)
g = percepatan gravitasi
h = ketinggian air
-
Teorema Toricelli (laju effluk)
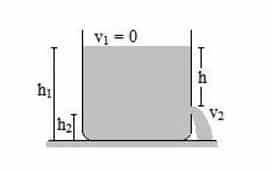
Laju air yang menyembur dfari lubang sama dengan air yang jatuh bebas dari ketinggianh. Laju air yang menyembur dari lubang dinamakan laju effluk. Fenomena ini dinamakan dengan teorema Toricelli.
Kita terapkan persamaan Bernoulli pada titik 1 (permukaan wadah) dan titik 2 (permukaan lubang). Karena diameter kran/lubang pada dasar wadah jauh lebih kecil dari diameter wadah, maka kecepatan zat cair di permukaan wadah dianggap nol (v1 = 0). Permukaan wadah dan permukaan lubang/kran terbuka sehingga tekanannya sama dengan tekanan atmosfir (P1 = P2). Dengan demikian, persamaan Bernoulli untuk kasus ini adalah :
Berdasarkan persamaan ini, tampak bahwa laju aliran air pada lubang yang berjarak h dari permukaan wadah sama dengan laju aliran air yang jatuh bebas sejauh h (bandingkan Gerak jatuh Bebas) Ini dikenal dengan Teorema Torricceli.
-
Venturimeter
Venturimeter adalah sebuah alat yang bernama pipa venturi. Pipa venturi merupakan sebuah pipa yang memiliki penampang bagian tengahnya lebih sempit dan diletakkan mendatar dengan dilengkapi dengan pipa pengendali untuk mengetahui permukaan air yang ada sehingga besarnya tekanan dapat diperhitungkan. Ada dua venturimeter yang akan kita pelajari, yaitu venturimeter tanpa manometer dan venturimeter menggunakan manometer yang berisi zat cair lain.
-
Tabung pitot
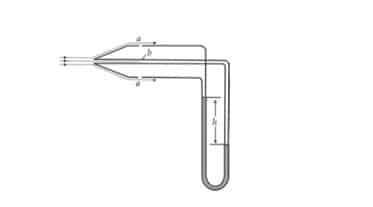
Alat ukur yang dapat kita gunakan untuk mengukur kelajuan gas adalah tabung pitot. Perhatikan gambar berikut.
Gas (misalnya udara) mengalir melalui lubanglubang di titik a. Lubang-lubang ini sejajar dengan arah aliran dan dibuat cukup jauh di belakang sehingga kelajuan dan tekanan gas di luar lubang-lubang tersebut mempunyai nilai seperti halnya dengan aliran bebas. Jadi, va = v (kelajuan gas) dan tekanan pada kaki kiri manometer tabung pilot sama dengan tekanan aliran gas (Pa).
Lubang dari kaki kanan manometer tegak lurus terhadap aliran sehingga kelajuan gas berkurang sampai ke nol di titik b (vb = 0). Pada titik ini gas berada dalam keadaan diam. Tekanan pada kaki kanan manometer sama dengan tekanan di titik b (pb). Beda ketinggian titik a dan b dapat diabaikan (ha = hb), sehingga perbedaan tekanan yang terjadi menurut persamaan Bernoulli adalah sebagai berikut :
- Penyemprot
Pada alat penyemprot alat nyamuk dan parfum, saat batang penghisap ditekan, udara akan mengalir dengan kecepatan tinggi dfan melewati dimulut pipa. Akibatnya ,tekanan diujung mulut pipa menjadi kecil. Perbedaan tekanan ini mengaklibatkan cairan didalam tangki naik dan dihamburkan dengan halus oleh aliran udara dari tabung pengisap.
- Pesawat Terbang
Gaya angkat pesawat terbang bukan karena mesin, tetapi pesawat bisa terbang karena memanfaatkan hukum bernoulli yang membuat laju aliran udara tepat di bawah sayap, karena laju aliran di atas lebih besar maka mengakibatkan tekanan di atas pesawat lebih kecil daripada tekanan pesawat di bawah.
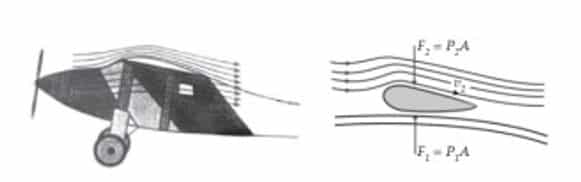
Penampang sayap pesawat terbang mempunyai bagian belakang yang lebih tajam dan sisi bagian atas yang lebih melengkung daripada sisi bagian bawahnya. Perhatikan gambar dibawah. Garis arus pada sisi bagian atas lebih rapat daripada sisi bagian bawahnya.
Artinya, kelajuan aliran udara pada sisi bagian atas pesawat v2 lebih besar daripada sisi bagian bawah sayap v1. Sesuai dengan asas Bornoulli, tekanan pada sisi bagian atas p2 lebih kecil daripada sisi bagian bawah p1 karena kelajuan udaranya lebih besar. Dengan A sebagai luas penampang pesawat, maka besarnya gaya angkat dapat kita ketahui melalui persamaan berikut.
Keterangan :
ρ = massa jenis udara (kg/m3)
va= kecepatan aliran udara pada bagian atas pesawat (m/s)
vb= kecepatan aliran udara pada bagian bawah pesawat (m/s)
F= Gaya angkat pesawat (N)
Pesawat terbang dapat terangkat ke atas jika gaya angkat lebih besar daripada berat pesawat. Jadi, suatu pesawat dapat terbang atau tidak tergantung dari berat pesawat, kelajuan pesawat, dan ukuran sayapnya. Makin besar kecepatan pesawat, makin besar kecepatan udara. Hal ini berarti gaya angkat sayap pesawat makin besar.
Demikian pula, makin besar ukuran sayap makin besar pula gaya angkatnya. Supaya pesawat dapat terangkat, gaya angkat harus lebih besar daripada berat pesawat (F1 – F2) > m g. Jika pesawat telah berada pada ketinggian tertentu dan pilot ingin mempertahankan ketinggiannya (melayang di udara), maka kelajuan pesawat harus diatur sedemikian rupa sehingga gaya angkat sama dengan berat pesawat (F1 – F2) = m g.
Contoh Soal dan pembahasan : Fluida Dinamis
Contoh Soal dan Pembahasan tentang Fluida Dinamis, Materi Fisika kelas 2 SMA. Mencakup debit, persamaan kontinuitas, Hukum Bernoulli dan Toricelli.
Contoh Soal No. 1
Ahmad mengisi ember yang memiliki kapasitas 20 liter dengan air dari sebuah kran seperti gambar berikut!
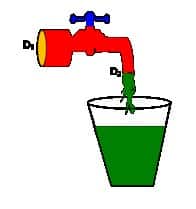
Jika luas penampang kran dengan diameter D2 adalah 2 cm2 dan kecepatan aliran air di kran adalah 10 m/s tentukan:
a) Debit air
b) Waktu yang diperlukan untuk mengisi ember
Pembahasan
Data :
A2 = 2 cm2 = 2 x 10−4 m2
v2 = 10 m/s
a) Debit air
Q = A2v2 = (2 x 10−4)(10)
Q = 2 x 10−3 m3/s
b) Waktu yang diperlukan untuk mengisi ember
Data :
V = 20 liter = 20 x 10−3 m3
Q = 2 x 10−3 m3/s
t = V / Q
t = ( 20 x 10−3 m3)/(2 x 10−3 m3/s )
t = 10 sekon
Soal No. 2
Pipa saluran air bawah tanah memiliki bentuk seperti gambar berikut!
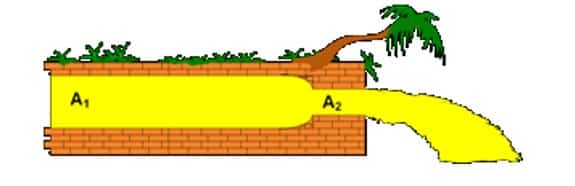
Jika luas penampang pipa besar adalah 5 m2 , luas penampang pipa kecil adalah 2 m2 dan kecepatan aliran air pada pipa besar adalah 15 m/s, tentukan kecepatan air saat mengalir pada pipa kecil!
Pembahasan
Persamaan kontinuitas
A1v1 = A2v2
(5)(15) = (2)v2
v2 = 37,5 m/s
Soal No. 3
Tangki air dengan lubang kebocoran diperlihatkan gambar berikut!
Jarak lubang ke tanah adalah 10 m dan jarak lubang ke permukaan air adalah 3,2 m. Tentukan :
a) Kecepatan keluarnya air
b) Jarak mendatar terjauh yang dicapai air
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah
Pembahasan
a) Kecepatan keluarnya air
v = √(2gh)
v = √(2 x 10 x 3,2) = 8 m/s
b) Jarak mendatar terjauh yang dicapai air
X = 2√(hH)
X = 2√(3,2 x 10) = 8√2 m
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah
t = √(2H/g)
t = √(2(10)/(10)) = √2 sekon
Soal No. 4
Untuk mengukur kecepatan aliran air pada sebuah pipa horizontal digunakan alat seperti diperlihatkan gambar berikut ini!
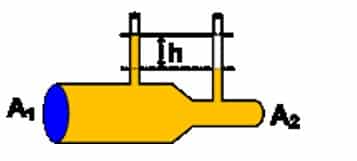
Jika luas penampang pipa besar adalah 5 cm2 dan luas penampang pipa kecil adalah 3 cm2 serta perbedaan ketinggian air pada dua pipa vertikal adalah 20 cm tentukan :
a) kecepatan air saat mengalir pada pipa besar
b) kecepatan air saat mengalir pada pipa kecil
Pembahasan
a) kecepatan air saat mengalir pada pipa besar
v1 = A2√ [(2gh) : (A12 − A22) ]
v1 = (3) √ [ (2 x 10 x 0,2) : (52 − 32) ]
v1 = 3 √ [ (4) : (16) ]
v1 = 1,5 m/s
Tips :
Satuan A biarkan dalam cm2 , g dan h harus dalam m/s2 dan m. v akan memiliki satuan m/s.
b) kecepatan air saat mengalir pada pipa kecil
A1v1 = A2v2
(3 / 2)(5) = (v2)(3)
v2 = 2,5 m/s
Soal No. 5
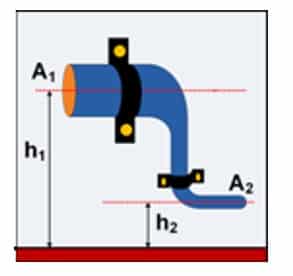
Pipa untuk menyalurkan air menempel pada sebuah dinding rumah seperti terlihat pada gambar berikut! Perbandingan luas penampang pipa besar dan pipa kecil adalah 4 : 1.
Posisi pipa besar adalah 5 m diatas tanah dan pipa kecil 1 m diatas tanah. Kecepatan aliran air pada pipa besar adalah 36 km/jam dengan tekanan 9,1 x 105 Pa. Tentukan :
a) Kecepatan air pada pipa kecil
b) Selisih tekanan pada kedua pipa
c) Tekanan pada pipa kecil
(ρair = 1000 kg/m3)
Pembahasan
Data :
h1 = 5 m
h2 = 1 m
v1 = 36 km/jam = 10 m/s
P1 = 9,1 x 105 Pa
A1 : A2 = 4 : 1
a) Kecepatan air pada pipa kecil
Persamaan Kontinuitas :
A1v1 = A2v2
(4)(10) = (1)(v2)
v2 = 40 m/s
b) Selisih tekanan pada kedua pipa
Dari Persamaan Bernoulli :
P1 + 1/2 ρv12 + ρgh1 = P2 + 1/2 ρv22 + ρgh2
P1 − P2 = 1/2 ρ(v22 − v12) + ρg(h2 − h1)
P1 − P2 = 1/2(1000)(402 − 102) + (1000)(10)(1 − 5)
P1 − P2 = (500)(1500) − 40000 = 750000 − 40000
P1 − P2 = 710000 Pa = 7,1 x 105 Pa
c) Tekanan pada pipa kecil
P1 − P2 = 7,1 x 105
9,1 x 105 − P2 = 7,1 x 105
P2 = 2,0 x 105 Pa
Contoh Untuk mengetahui bagaimana penerapan fluida dinamis dalam kehidupan sehari-hari :
Dalam kehidupan sehari-hari, dapat ditemukan aplikasi Hukum Bernoulli yang sudah banyak diterapkan pada sarana dan prasarana yang menunjang kehidupan manusia masa kini seperti :
- untuk menentukan gaya angkat pada sayap dan badan pesawat terbang
- penyemprot parfum
- penyemprot racun serangga
Itulah ulasan tentang Fluida Dinamis : Pengertian, Jenis Aliran, Ciri Dan Rumus Beserta Contoh Soalnya Lengkap Semoga apa yang diulas diatas bermanfaat. sekian dan terimakasih.
Baca juga refrensi artikel terkait lainnya disini :
- Makalah Ikatan Kimia : Pengertian, Jenis Beserta Gambarnya Lengkap
- Induksi Elektromagnetik : Pengertian, Penerapan, dan Rumus Beserta Contoh Soalnya Secara Lengkap
- Arus Bolak-Balik : Pengertian, Keuntungan, Dan Contoh Soalnya Lengkap
Link Sponsor