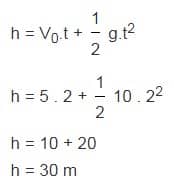Tahukah anda apa yang dimaksud dengan Gerak Vertikal Ke Bawah ??? Jika anda belum mengetahuinya anda tepat sekali mengunjungi gurupendidikan.com. Karena pada kesempatan kali ini akan membahas tentang pengertian Gerak Vertikal Ke Bawah, ciri Gerak Vertikal Ke Bawah, dan rumus Gerak Vertikal Ke Bawah beserta contoh soal Gerak Vertikal Ke Bawah secara lengkap. Oleh karena itu marilah simak ulasan yang ada dibawah berikut ini.
Pengertian Gerak Vertikal Ke Bawah
Berbeda dengan jatuh bebas, gerak vertikal ke bawah yang dimaksudkan adalah gerak benda-benda yang dilemparkan vertikal ke bawah dengan kecepatan awal tertentu. Jadi seperti gerak vertikal ke atas hanya saja arahnya ke bawah. Sehingga persamaan-persamaannya sama dengan persamaan-persamaan pada gerak vertikal ke atas, kecuali tanda negatif pada persamaan-persamaan gerak vertikal ke atas diganti dengan tanda positif.
Ciri-Ciri Gerak Vertikal Ke Bawah
Pada dasarnya gerak jatuh bebas merupakan gerak vertikal ke bawah tanpa kecepatan awal. itu artinya ciri-ciri vertikal ke bawah tidak jauh dari gerak jatuh bebas. Yang membedakan hanya besar kecepatan awal saja.
Suatu benda bergerak vertikal ke bawah jika mempunyai ciri-ciri sebagai berikut :
- Benda bergerak atau dilemapar dari ketinggian tertentu diatas permukaan tanah
- lintasan benda berpa garis lurus dalam arah vertikal
- memiliki kecepatan awal
- perhitungan benda dihitung dari titik tertinggi
- Percepatan benda sama dengan percepatan gravitasi (a=+g)
Rumus Gerak Vertikal Ke Bawah
Persamaan pada GVB diperoleh dari persamaan GLBB.
Vt = V0 + g.t
h = V0t + ½ gt2
Vt2= V02 + 2gh
Keterangan:
Vt = Kecepatan pada saat t (m/s)
V0 = Kecepatan awal (m/s)
g = percepatan gravitasi (m/s2)
h = ketinggian (m)
t = Waktu(s)
Dalam gerak vertikal ke bawah (GVB) terdapat sejumlah rumus pokok yang dapat dipakai untuk menuntaskan soal-soal fisika yang bersangkutan dengan gerak vertikal ke atas. Rumus-rumus itu yaitu:
1. Rumus Kecepatan Awal dan Kecepatan Akhir Benda
Gerak vertikal ke atas (GVA) adalahgerak benda dari elevasi nol (posisi awal) mengarah ke ke atas dan bakal tiba di sebuah titik yang dinamakan titik tertinggi. Titik tertinggi ialah ketinggian maksimum atau eksodus terbesar yang dapat dijangkau oleh benda.
Agar bisa bergerak ke atas, benda mesti mempunyai kecepatan awal, sampai-sampai nilai kecepatan mula benda tidak sama dengan nol. Kecepatan mula pada gerak vertikal ke atas bakal mempengaruhi elevasi maksimum yang dapat dijangkau oleh benda. Semakin besar kecepatan mula maka semakin besar elevasi maksimumnya.
Perhatikan gambar di atas. Misalkan suatu benda bergerak vertikal ke atas dengan kecepatan mula v0. Saat mendarat dititik tertentu kecepatannya menurun menjadi vt dampak pengaruh percepatan gravitasi. Kecepatan benda bakal terus menurun hingga akhirnya kecepatannya menjadi nol, yakni pada titik tertinggi.
Kecepatan pada titik tertinggi berikut yang disebut percepatan akhir benda yang bergerak vertikal ke atas.
v = 0
Keterangan:
v0 = kecepatan mula benda (m/s)
v = kecepatan akhir benda (m/s)
2. Rumus Percepatan Benda
Seperti pada dua jenis gerak vertikal yang telah dibicarakan sebelumnya yakni GJB dan GVB, pada gerak vertikal ke atas (GVA), percepatan yang dirasakan benda pun adalahpercepatan gravitasi. Namun sebab arah gerak benda ke atas melawan arah gravitasi bumi, maka percepatan gravitasi bumi bermanfaat sebagai perlambatan.
Perlambatan adalah percepatan yang bernilai negatif sampai-sampai percepatan negatif berikut yang mengakibatkan kecepatan benda menurun. Pada gambar di atas mengindikasikan nilai percepatan gerak benda sama dengan besar percepatan gravitasi bumi yang bernilai negatif.
a = -g
Keterangan:
g = 9,8 m/s2 atau 10 m/s2
Jika dalam soal nilai g tidak diketahui, maka kita pakai nilai 10 m/s2 sebagai nilai percepatan gravitasi pada gerak jatuh bebas atau jenis gerak vertikal lainnya.
3. Rumus Perpindahan dan Ketinggian Benda
Dalam gerak vertikal, elevasi (h) diukur dari tanah atau lantai mengarah ke posisi benda pada elevasi tertentu. Perhatikan gambar di atas, pada gerak vertikal ke atas, eksodus (s) benda diukur dari posisi mula benda (di lantai) mengarah ke posisi benda pada elevasi tertentu.
Jadi dalam gerak vertikal ke atas, eksodus benda sama dengan ketinggiannya. Itu sebabnya, eksodus dalam gerak vertikal disimbolkan dengan h. Dengan mensubtitusikan persamaan 4 dan 6 ke persamaan 2, maka besar eksodus atau elevasi benda pada gerak vertikal ke atas bisa dihitung dengan rumus:
|
s
|
=
|
s0 + v0t ± ½ at2
|
|
|
h
|
=
|
0 + v0t − ½ gt2
|
|
|
h
|
=
|
v0t − ½ g.t2
|
Keterangan :
h = perpindahan atau ketinggian (m)
v0 = kecepatan awal (m/s)
g = percepatan gravitasi bumi (m/s2)
t = waktu (s)
4. Rumus Kecepatan Setelah t Detik
Karena arah gerak melawan arah gravitasi, maka benda merasakan perlambatan atau nilai percepatannya negatif. Jika kecepatan mula benda v0 dan kecepatan benda pada t detik ialah vt maka dengan mensubtitusikan persaman 6 ke persamaan 1, formula kecepatan benda sesudah t detik pada GVA ialah sebagai berikut:
|
vt
|
=
|
v0 ± at
|
|
|
vt
|
=
|
v0 − gt
|
Sedangkan andai persamaan 4 dan 5 anda subtitusikan ke persamaan 3 maka anda akan mendapatkan formula kecepatan sesudah t detik sebagai berikut:
|
vt2
|
=
|
v02 ± 2as
|
|
|
vt2
|
=
|
v02 − 2gh
|
Keterangan:
vt = kecepatan benda setelah t detik (m/s)
v0 = kecepatan awal (m/s)
g = percepatan gravitasi bumi (m/s2)
t = waktu (s)
h = perpindahan benda (m)
Contoh Soal Gerak Vertikal Ke Bawah
Contoh 1
Bola dilempar vertikal kebawah dari sebuah bangunan bertingkat dengan kelajuan awal 10 m/s dan tiba ditanah setelah 2 sekon. Kelajuan bola ketika menyentuh tanah yaitu ???
Pembahasan:
Diketahui:
v0 = 10 m/s
t = 2 sekong = 10 m/s2
Ditanya: v = …???
Jawab:
v = v0 + g . t = 10 m/s + 10 m/s2 . 2 s = 10 m/s + 20 m/s = 30 m/s
Jadi, kelajuan bola ketika menyentuh tanah 30 m/s
Contoh 2
Seorang anak melempar batu ke dalam sumur dengan kecepatan awal 5 m/s dan menyentuh permukaan air setelah 2 detik. Hitunglah kedalaman sumur tersebut ?
Pembahasan
Jadi kedalaman sumur tersebut adalah 30 meter.
Contoh 3
Sebuah kotak kecil dilemparkan dari sebuah bangunan dengan ketinggian 80 meter dan kecepatan awal 10 m/s. Berapa lama waktu yang diperlukan oleh kotak tersebut mencapai tanah ?
Pembahasan
Vt2 = V02 + 2 . g . h
Vt2 = 102 + 2 . 10 . 80
Vt2 = 100 + 1600
Vt2 = 1700 m/s
Masukkan nilai Vt ke persamaan berikut :
Vt = V0 + g.t
41 = 10 + 10.t
10t = 31
t = 3,1 detik
Jadi waktu yang diperlukan kotak tersebut mencapai tanah adalah 2,1 detik.
Contoh 4
Pada ketinggian 60 meter, sebuah benda bergerak secara vertikal ke bawah. Jika diberikan kecepatan awal sebesar 10 m/s, berapakah kecepatan benda pada saat ketinggian 20 m di atas tanah.
Pembahasan
Vt2 = V02 + 2 . g . h
Vt2 = 102 + 2 . 10 . (60-20)
Vt2 = 100 + 800
Vt2 = 900 m/s
Jadi kecepatan benda tersebut pada ketinggian 20 m adalah 900 m/s
Contoh 5
Sebuah bola dilemparkan vertikal ke bawah dari jendela hotel dengan kecepatan awal 4 m/s. Pada jarak berapakan dibawah jendela hotel kecepatan bola menjadi dua kali kecepatan awal ?
Pembahasan
Vt2 = V02 + 2 . g . h
Karena ditanya pada jarak berapakah (tinggi), kecepatan bola menjadi dua kali kecepatan awal, maka persamaannya menjadi :
(2V0)2 = V02 + 2 . g . h
(2.4)2 = 42 + 2 . 10 . h
(8)2 = 16 + 20h
20h = 64 – 16
20 h = 48
h = 48/20
h = 2,4 m
Baca Juga :
- Gerak Vertikal Ke Atas : Pengertian, Ciri, Dan Rumus Beserta Contohnya Secara Lengkap
- Gerak Jatuh Bebas : Pengertian, Rumus, Dan Contoh Soalnya Secara Lengkap
- Pengertian, Ciri, Dan Rumus Gerak Lurus Beraturan Beserta Contohnya Secara Lengkap
- Pengertian, Ciri, Dan Rumus Gerak Lurus Berubah Beraturan (GLBB) Secara Lengkap.
- Pengertian, Rumus Dan Contoh Soal Tekanan Udara Beserta Alat Ukurnya Lengkap.
- Pengertian, Manfaat Dan Kerugian Kapaliritas Beserta Contohnya Dalam Kehidupan Sehari-hari.