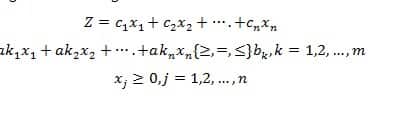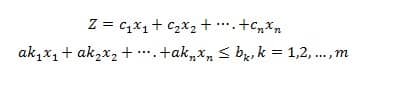Penegertian Linear Programing – Tujuan, Model, Fungsi, Langkah, Bentuk, Metode, Para Ahli : Dalam kasus program linear, fungsi objektif dan kendala adalah semua fungsi linear dari variabel keputusan.
Penegertian Linear Programing
Dalam suatu penetapan jumlah dan juga jenis produksinya yang harus dihasilkan oleh suatu perusahaan untuk periode tertentu dapat menggunakan suatu metode linier programming. Dengan metode linier programming tersebut perusahaan dapat menentukan kombinasi produk yang akan dihasilkan oleh suatu perusahaan dengan kapasitas produksi yang dipunyai perusahaan.
Baca Juga Artikel Yang Mungkin Berhubungan : Peranan Media Massa Dalam Komunikasi Politik Beserta Proses Dan Modelnya
Dalam sebuah program mathematika terdapat sebuah fungsi objektif tunggal, yang mempresenting sehingga laba menjadi maksimal atau membuat agar harga menjadi minimal, dan kendala yang membatasi variabel keputusan. Dalam kasus program linear, fungsi objektif dan kendala adalah semua fungsi linear dari variabel keputusan. Program linear secara luas menggunakan tipe model yang dapat menyelesaikan masalah keputsan dengan beribu variabel.
Pengertian Linear Programing Menurut Para Ahli
Banyak Sekali Definisi Menurut Para Ahli , antara lain ialah sebagai berikut :
-
T. Hani Handoko (1999, p379) :
Linear Programing ialah suatu metode analitik paling terkenal dan yang merupakan suatu bagian pada kelompok teknik-teknik yang disebut dengan programisasi matematik.
-
Sofjan Assauri (1999, p9) :
pengertian linear Programing ialah suatu teknik perencanaan yang dengan menggunakan model matematika dengan tujuan untuk menemukan kombinasi-kombinasi produk yang terbaik didalam menyusun suatu alokasi sumber daya yang terbatas guna untuk mencapai tujuan yang digunakan dengan secara optimal.
-
Zainal Mustafa, EQ, dan juga Ali Parkhan (2000, p43)
Linear Programing ialah suatu cara yang lazim digunakan dalam pemecahan suatu masalah pengalokasian sumber-sumber yang terbatas dengan secara optimal.
-
Zulian Yamit (1996, p14) :
Linear programming ialah metode ataupun teknik matematis yang digunakan untuk dapat membantu manajer dalam pengambilan keputusan. Ciri khusus dalam penggunaan metode matematis ini ialah berusaha untuk mendapatkan maksimisasi atau juga minimisasi.
Tujuan Linear Programing
Tujuan Linear Programing ialah mencari pemecahan persoalan-persoalan yang timbul didalam perusahaan, yakni mencari keadaan yang optimal dengan cara memperhitungkan batasan yang ada.
Model Linear Programing
Ciri khas model linear programming ialah bahwa linear programming tersebut didukung oleh macam-macam asumsi yang menjadikan sebagai tulang punggung model tersebut. Asumsi tersebut antara lain ialah sebagai berikut :
Baca Juga Artikel Yang Mungkin Berhubungan : Pengertian Media Komunikasi Menurut Para Ahli Beserta Jenis Dan Fungsinya
-
Propotionality
Pada Asumsi ini ialah bahwa naik turunnya nilai z dan juga penggunaan faktor-faktor produksi yang tersedia akan dapat berubah secara sebanding atau sejajar (proposional) pada perubahan tingkat kegiatan.
-
Additivity
Pada Asumsi ini ialah bahwa nilai tujuan pada tiap kegiatan tidak saling mempengaruhi satu sama lain, atau dalam linear programming tersebut dianggap bahwa suatu kenaikan nilai tujuan yang diakibatkan oleh kenaikan suatu kegiatan(proses) dapat ditumbuhkan dengan tidak harus mempengaruhi nilai Z yang diperoleh dari kegiatan lain.
-
Divisibility
Pada Asumsi ini menyatakan bahwa suatu keluaran (output) yang dihasilkan oleh suatu kegiatan(proses) dapat berupa suatu bilangan pecahan, demikian juga dengan nilai Z yang dihasilkan.
-
Deterministic (certainty)
Pada Asumsi ini menyatakan bahwa semua parameter yang terdapat didalam model linear programming (aij, bj, cj ) tersebut dapat diperkirakan dengan pasti walaupun jarang digunakan tepat.
Fungsi Linear Programming
Dalam model linear programming dikenal 2 macam fungsi :
1. Fungsi Tujuan (objective Function)
Fungsi tujuan ialah fungsi yang menggambarkan suatu tujuan ataupun sasaran ataujuga target didalam suatu permasalahan linear programming yang berkaitan dengan suatu peraturan dengan secara optimal sumber daya(resource) untuk memperoleh suatu keuntungan yang maksimal.
2. Fungsi Batasan (Constraint Function)
Fungsi ialah suatu bentuk penyajian dengan secara sistematis batasan-batasan suatu kapasitas yang tersedia akan dapat dialokasikan secara optimal. Masalah linear programming tersebut dapat dinyatakan ialah sebagai proses optimisasi suatu fungsi tujuan didalam bentuk Memaksimumkan ataupun meminimumkan.
Baca Juga Artikel Yang Mungkin Berhubungan : 21 Ciri, Pengertian Media Sosial Menurut Para Ahli & Dampak Positif Negatifnya
Langkah-langkah perumusan masalah pemrograman linier ( LPP).
Langkah-langkah berikut yang terlibat dalam perumusan linear programming probel ( LPP).
- Langkah 1 : mengidentifikasi variabel keputusan masalah.
- Langkah 2 : membangun fungsi tujuan sebagai kombinasi lonear dari variabel keputusan ,
- Langkah 3 mengidentifikasi kendala dari masalah seperti sumber daya , limitions , antar – hubungan antara variabel , dll Merumuskan kendala ini sebagai persamaan linear atau inequations dalam hal variabel keputusan non negatif.
Dengan demikian , LPP adalah kumpulan fungsi tujuan , himpunan kendala dan set non -negatif kendala.
Bentuk Umum LPP
LPP umum dapat digambarkan sebagai berikut :
Diberikan satu set m – linear kesenjangan atau persamaan dalam n – variabel , kita ingin mencari nilai-nilai non-negatif dari variabel-variabel yang akan memenuhi kendala dan mengoptimalkan ( memaksimalkan atau meminimalkan ) fungsi linier dari variabel-variabel ( fungsi tujuan ).
Secara matematis , kami memiliki kesenjangan m – linear dengan n – variabel (m dapat lebih besar dari , kurang dari atau sama dengan n ) dari bentuk tersebut. Untuk setiap kendala, hanya satu dari tanda-tanda ini (≥, = , ≤) digunakan, tapi dapat bervariasi dari satu kendala kepada kendala yang lain untuk mencari nilai variabel Xj memenuhi ( 3.1 ) dan yang memaksimalkan atau meminimalkan fungsi linea.
LPP dalam Bentuk Canonical
secara umum ≤ kendala akan dikaitkan dengan maksimalisasi LPP dan ≥ kendala dengan minimalisasi LPP.
Maksimalisasi :
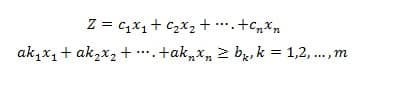 Catatan: kendala yang berbeda mungkin memiliki tanda-tanda yang berbeda
Catatan: kendala yang berbeda mungkin memiliki tanda-tanda yang berbeda
Catatan: ketika tidak ada disebutkan tentang kenegativan variabel, maka terbatas dalam tanda atau diabaikan.
Baca Juga Artikel Yang Mungkin Berhubungan : “Media Massa” Pengertian & ( Jenis – Karakteristik – Fungsi – Perkembangan )
Metode Grafis
Masalah Program linear yang memiliki dua variabel keputusan bisa di selesaikan dengan menggunakan metode grafis. dengan menggunakan hasil yang telah dibuktikan pada seksi 3.3, solusi yang optimal untuk menyelesaikannya dapat ditemukan dengan mengevaluasi fungsi objektif untuk setiap titik puncak dari daerah yang dikerjakan. Adapun cara pengerjaan Masalah Program Linear dengan metode grafis ini dapat diliat seperti berikut :
-
Pendekatan titik ekstrim
langkah 1 : Rumuskan Masalah Program Linear seperti yang telah didiskusikan pada bagian 3.2
langkah 2 : letakkan semua pembatas pada kertas grafis dan bayangan dari daerah yang memungkinkan untuk dikerjakan
langkah 3 : catat semua titik ekstrim pada daerah yang dikerjakan kemudian evaluasi nilai dari fungsi objektif pada setiap titik ekstrik tersebut.
- Pendekatan fungsi garis Iso-Profit (harga)
Setelah mengikuti langkah 1 dan 2 pada bagian 3.4.1 :
langkah 3 : gambar sebuah garis iso-profit (iso-harga) untuk nilai kecil dari fungsi objektif tanpa melanggar batas dari masalah yang telah diberikan.
langkah 4 : pindahkan garis paralel iso-profit (iso-cost) dalam arah peningkatan (atau penurunan) fungsi objektif.
langkah 5 : titik ekstrim yang dipindahakn merupakan solusi optimal.
Pengganti (atau ganda) solusi optimal
Pada kasus ini garis iso-profit bertepatan dengan ujung dari daerah yang dikerjakan. Jadi, disana akan terdapat banyak titik yang tak terbatas yang mana fungsi objektif nya maksimum. Dengan demikian,garis iso-profit akan memberikan solusi optimal dan solusi ini akan menghasilkan nilai yang sama dengan nilai fungsi objektif.
-
Solusi tak terbatas
Ketika nilai variabel yang ditentukan dalam program linear meningkat tak terbatas tanpa melanggar daerah yang dikerjakan, solusi nya bisa dikatan tak tebatas.
-
Solusi tak dapat dibatalkan
Hal ini dapat terjadi ketika tidak ada nilai dari variable yang memuaskan semua pembatas secara serempak;kesamaan.
Baca Juga Artikel Yang Mungkin Berhubungan : Perilaku Menyimpang : Pengertian, Ciri, Dan Jenis Beserta Contohnya Secara Lengkap