Pengertian Ukuran Nilai Pusat, Jenis, Sifat, Rumus dan Contoh Adalah ukuran yang dapat mewakili data secara keseluruhan. Artinya, jika keseluruhan nilai yang ada dalam data
Baca Juga Artikel Yang Mungkin Berhubungan : Pengertian Pendapatan – Konsep, Jenis, Sumber, Karakteristik, Pengukuran, Kriteria, Para Ahli
Pengertian Nilai Pusat
Merupakan ukuran yang dapat mewakili data secara keseluruhan. Artinya, jika keseluruhan nilai yang ada dalam data tersebut diurutkan besarnya dan selanjutnya dimasukkan nilai rata-rata ke dalamnya, nilai rata-rata tersebut memiliki kecenderungan terletak di urutan paling tengah.
Dalam keperluan penganalisaan data lebih lanjut di perlukan juga ukuran-ukuran yang dapat mewakili data tersebut, sehingga dapat di ucapkan dengan singkat serta dapat digunakan untuk membandingkan keadaan berbagai kelompok data.
Nilai Tunggal yang dianggap dapat mewakili keseluruhan nilai dalam sebuah data dianggap sebagi rata-rata (averages) , dikarenakan nilai rata-rata itu dihitung berdasarkan keseluruhan nilai yang terdapat dalam data yang bersangkutan.
Tujuan: Mengukur besarnya nilai pemusatan dari distribusi data yang telah diperoleh dalam penelitian.
Baca Juga Artikel Yang Mungkin Berhubungan : Biologi Molekul – Pengertian, Teknik, Ilmu, Sejarah, Ukuran, Rumus, Geometri
Sifat Ukuran Nilai Pusat
Sifat-Sifat Mean
- Nilai rata-rata hitung dipengaruhi oleh observasi atau pengamatan.
- Nilai rata-rata hitung dapat menyimpang terlalu jauh.
- Rata-rata hitung tidak dapat dihitung dari distribusi yang memiliki kelas terbuka.
- Rata-rata paling sering digunakan dan populer, sehingga penjelasan mengenai arti rata-rata hitung tidak diperlukan.
- Jumah dari penyimpangan semua nilai pengamatan dengan nilai rata-rata hitung sama dengan nol.
- Jika selisih semua nilai pengamatan dengan nilai rata- rata dihitung dikuadratkan maka jumlahnya lebih kecil daripada jumlah penyimpangan kuadrat semua nilai pengamatan dari titik lain selain rata-rata hitung.
- Rata-rata hitung dapat memanipulasi secara aljabar.
Sifat-Sifat Median
- Median dipengaruhi oleh banyaknya observasi, namun tidak dipengaruhi oleh nilai pengamatan.
- Median dapat dihitung dari distribusi yang memiliki kelas terbua, kecuali jika kelas mediannya berada pada kelas terbuka tersebut.
- Median sering digunakan pada distribusi yang memiliki kecondongan yang sangat jelek.
- Median didefinisikan dan diinterpretasikan.
- Median lebih terpengaruh oleh fluktuasi sampling, namun adakalanya untuk distribusi tertentu median lebih konstan terhadap fluktuasi sampling.
- Jumlah penyimpangan nilai-nilai dari median lebih kecil daripada jumlah penyimpangan nilai-nilai dari titik yang lain.
- Jika jumlah penyimpangan dari median dikuadratkan maka jumlahnya lebih besar daripada jumlah penyimpangan kuadrat nilai-nilai dari titik yang lain.
Sifat-Sifat Modus
- Dalam seperangkat data, modus bisa tidak ada dan bisa lebih dari satu.
- Modus dapat ditempatkan pada distribusi yang memiliki kelas terbuka.
- Modus tidak dipengaruhi oleh bilangan-bilangan yang ekstrim, dari suatu distribusi.
- Letak modus atau nilai modus yang sebenarnya sukar ditentukan, karena itu kebanyakan hanya berdasarkan taksiran dalam suatu distribusi.
- Perhitungan modus tidak didasarkan pada seluruh nilai pengamatan, tetapi didasarkan pada individu yang berada pada titik tempat terjadinya pemusatan yang terbanyak.
- Untuk perhitungan-perhitungan secara aljabar lebih lanjut, modus tidak dapat digunakan.
- Modus tidak sepopuler ukuran rata-rata hitung atau median.
Baca Juga Artikel Yang Mungkin Berhubungan : Pengertian Pendapatan – Konsep, Jenis, Sumber, Karakteristik, Pengukuran, Kriteria, Para Ahli
Jenis dan Macam Ukuran Nilai Pusat
Mean
Definisi : Penjumlahan nilai data pengamatan dibagi jumlah data pengamatan
Rata-Rata Hitung (mean)
Rata-Rata Hitung (mean) ini merupakan nilai rata-rata dari data-data yang ada.
terdapat 2 cara Rata-rata hitung yaitu :
- Rata-rata hitung (mean) data tunggal , dan .
- Rata-Rata Hitung (mean) data berkelompok.
untuk data berkelompok berkelompok ,Rata-Rata Hitung (mean) dihitung menggunakan 3 metode , metode tersebut iyalah :
- Metode biasa.
- Metode simpanan rata-rata.
- Metode Coding.
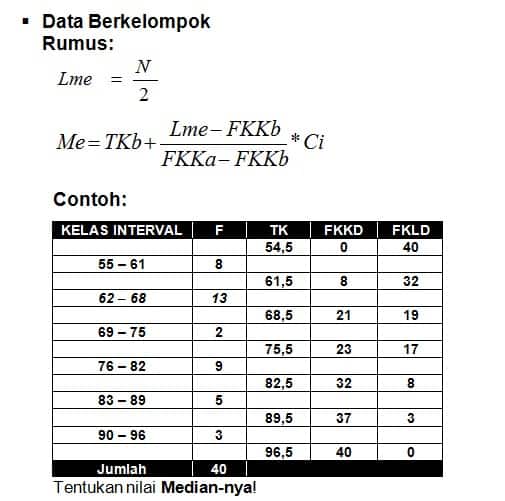
Median
Definisi: Ukuran rata-rata yang ukurannya didasarkan pada nilai data yang berada di tengah-tengah distribusi frekuensinya
Median Merupakan nilai tengah dari data yang ada setelah data di urutkan . median iyalah rata-rata apabila ditinjau dari segi kedudukannya dalam urutan data. median sering pula disebut rata-rata posisi.
Median dibedakan menjadi 2 kelompok yaitu.
- Median Data tunggal .
- Median Data berkelompok.
Data Tidak Berkelompok
Langkah-langkah:
- Urutkan datanya (ascending)
- Tentukan letak median
- Tentukan nilai median
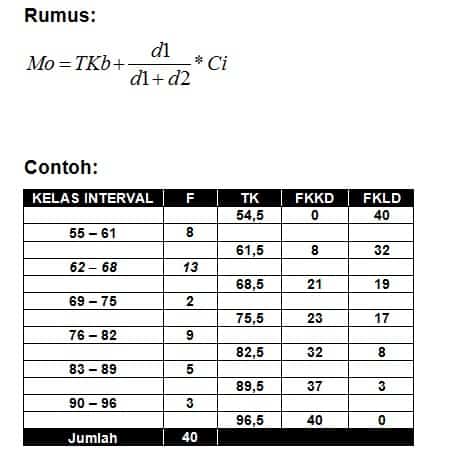
Modus
Definisi: Suatu pengamatan dalam distribusi frekuensi yang memiliki jumlah frekuensi paling besar
Modus iyalah nilai yang paling sering muncul dalam data. modus sering ditulis singkat atau disimbolkan dengan Mo . Sejumlah data bisa tidak memiliki modus , mempunyai satu modus disebut dengan Unimodal , mempunyai dua modus disebut dengan Bimodal , atau lebih dari dua modus disebut dengan Multimodal.
Modus dibedakan antara lain :
- Modus data tunggal , dan
- Modus data berkelompok.
Data Tidak Berkelompok
Contoh:
Data hasil pengamatan, sebagai berikut:
8, 7, 10, 11, 12, 15, 12, 11, 12, 6, 6, 12, 7 dan 12
Maka, modus-nya adalah 12 (muncul 5 kali)
Data Berkelompok
Contoh:
Data hasil pengamatan, sebagai berikut:
8, 7, 10, 11, 12, 15, 12, 11, 12, 6, 6, 12, 7 dan 12
Maka, modus-nya adalah 12 (muncul 5 kali)