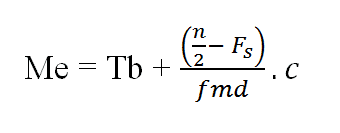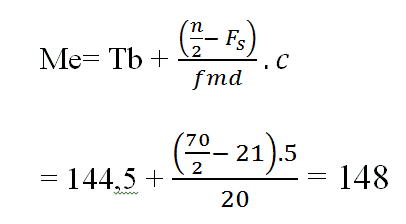Pengertian Mean, Median, Modus beserta Contoh

Pengertian Mean

Pengertian mean adalah teknik penjelasan kelompok yang didasarkan atas nilai rata-rata dari kelompok tersebut. Rata-Rata (mean) ini didapat dengan menjumlahkan data seluruh individu dalam kelompok itu, kemudian dibagi dengan jumlah individu yang ada pada kelompok tersebut. Ringkasnya, mean adalah nilai rata-rata dari sejumlah data.

Mean atau rataan merupakan nilai rata-rata dari sekumpulan data. Mean biasanya dinotasikan dengan huruf yang diatasnya terdapat garis, seperti x ̅, y ̅, dan v ̅.

Fungsi dan Sifat Mean

Beberapa sifat rata-rata hitung atau mean , antara lain sebagai berikut :

1. Nilai rata-rata hitung atau mean di pengaruhi oleh pengamatan atau observasi.
2. Nilai rata-rata atau mean dapat menyimpang terlalu jauh , dikarenakan rata-rata hitung di pengaruhi oleh bilangan-bilangan ekstream(nilai sangat besar atau nilai sangat kecil) , sehingga untuk distribusi dengan kecondongan yang jelek , rata- rata hitung atau mean dapat kehilangan makna.
3. Nilai rata-rata atau mean tidak dapat dihitung dari distribusi yang memiliki kelas terbuka.
4. Nilai rata-rata atau mean iyalah rata-rata yang paling populer , sehingga penjelasan mengenai arti rata-rata hitung tidak di perlukan.
5. Jumlah dari penyimpangan semua nilai pengamatan dengan nilai-nilai rata-rata hitung sama dengan nol.
6. Jika selisih semua nilai pengamatan dengan nilai rata-rata hitung dikuadratkan maka jumlah lebih kecil dari pada jumlah penyimpangan kuadrat semua nilai pengamatan dari titik lain selai rata-rata hitung.
7. Nilai rata-rata atau mean dapat dimanipulasi secara aljabar.

Rumus dan Contoh Soal Mean

---

• Data Tunggal
  

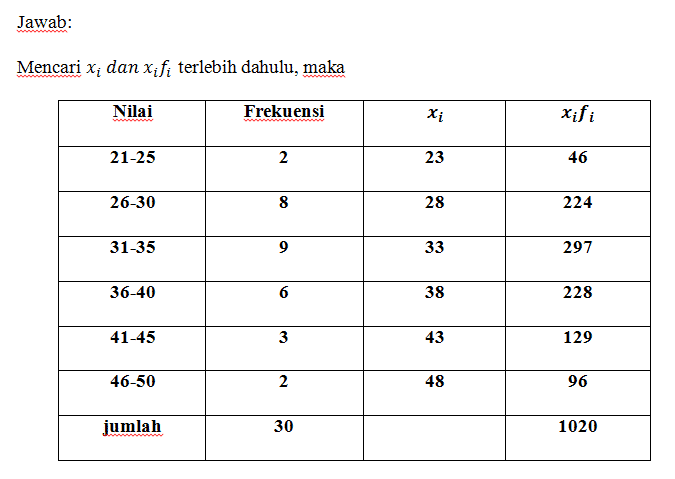
• Data Kelompok

---

Pengertian Median (Me)

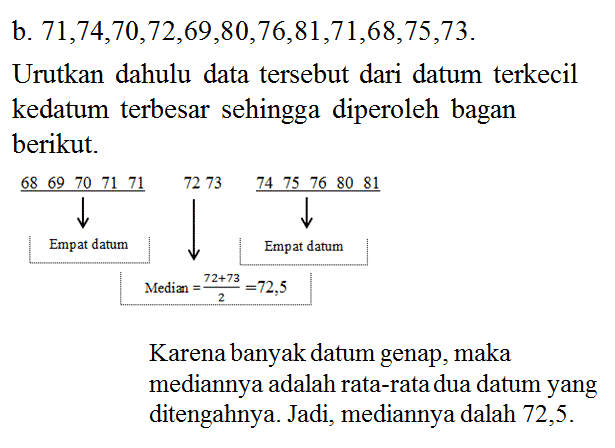
Median adalah nilai tengah dari data yang telah diurutkan dari datum terkecil ke datum terbesar

Median adalah nilai yang letaknya di tengah dari data yang telah diurutkan dari nilai terkecil sampai terbesar. Jika banyak data ganjil maka  median adalah data yang terletak tepat yang ditengah setelah diurutkan · Jika banyak data genap maka Me adalah ratarata dari dua data yang terletak di tengah setelah diurutkan.

Fungsi dan Sifat Median

Beberapa sifat-sifat median , antara lain sebagai berikut :

1. Median di pengaruhi oleh banyaknya observasi atau pengamatan, namun tidak dipengaruhi oleh nilai pengamatan, sehingga nilai median tidak dipengaruhi oleh bilangan-bilangan ekstream.
2. Median dapat dihitung dari distribusi yang memiliki kelas terbuka kecuali jika kelas mediannya berada pad kelas terbuka tersebut.
3. Median sering digunakan pada distribusi yang memiliki kecondongan yang sangat jelek.
4. Median didefinisikan dan diinterprestasikan .
5. Median lebih terpengaruh oleh fluktuasi sampling , namun adakalanya untuk distribusi tertentu median lebih konstan terhadap fluktuasi sampling,
6. Jumlah penyimpangan (tanda diabaikan) nilai-nilai dari median lebih kecil dari pada jumlah penyimpangan nilai-nilai dari titik yang laen.
7. Jika jumlah penyimpangan dari median dikuadratkan jumlah lebih besar dari pada jumlah penyimpangan kuadrat nilai-nilai dari rata-rata hitung atau mean.

---

Rumus dan Contoh Soal Mean

---

• Data Tunggal

• ---

  Data Kelompok

Keterangan

• Tb= tepi bawah kelas median
• Fs= jumlah frekuensi kelas-klas sebelum median
• Fmd= frekuensi kelas median
• C = panjang interval kelas
• n = banyaknya data

---

Pengertian Modus (Mo)

Modus adalah datum yang paling sering muncul. Dan biasanya dinotasikan dengan Mo

Modus adalah nilai yang sering muncul. Jika kita tertarik pada data frekuensi, jumlah dari suatu nilai dari kumpulan data, maka kita menggunakan modus. Modus sangat baik bila digunakan untuk data yang memiliki sekala kategorik yaitu nominal atau ordinal

Sedangkan data ordinal adalah data kategorik yang bisa diurutkan, misalnya kita menanyakan kepada 100 orang tentang kebiasaan untuk mencuci kaki sebelum tidur, dengan pilihan jawaban: selalu (5), sering (4), kadang-kadang(3), jarang (2), tidak pernah (1). Apabila kita ingin melihat ukuran pemusatannya lebih baik menggunakan modus yaitu yaitu jawaban yang paling banyak dipilih, misalnya sering (2). Berarti sebagian besar orang dari 100 orang yang ditanyakan menjawab sering mencuci kaki sebelum tidur.

Fungsi dan Sifat Modus

Beberapa sifat-sifat modus , antara lain sebagai berikut :

1. Dalam seperangkat data , modus bisa tidak ada dan bisa lebih dari satu.
2. Modus atau mode dapat ditempatkan pada distribusi yang memiliki kelas terbuka .
3. Modus atau mode tidak terpengaruhi oleh bilangan-bilangan ekstream ,  dari suatu distribusi.
4. letak modus atau nilai modus yang sebenarnya sukar ditemukan , karena itu kebanyakan hamya berdasarkan taksiran dalam suatu distribusi.
5. Perhitungan Modus atau mode tidak didasarkan pada seluruh nilai pengamatan, tetapi didasarkan pada individu yang berada pada titik terjadinya pemusatan yang banyak.
6. Untuk perhitungan perhitungan secar aljabar lebih lanjut , modus tidak dapat digunakan.
7. Modus atau mode tidak sepopuler ukuran rata rata hitung atau mean dan Median.

---

Rumus dan Contoh Soal Modus

• Modus Pada Data Kualitatif

Tahun 1970 di Yogyakarta, banyak mahasiswa yang naik sepeda. Sehingga dapat menjelaskan dengan modus, bahwa kelompok mahasiswa di Yogyakarta masih banyak yang naik sepeda.

• Modus Pada Data Kuantitatif

Umur pegawai kantor Y adalah : 20, 45, 60, 56, 45, 45, 20, 19, 57, 45, 45, 51, 35

Dari data diatas, dapat dilihat bahwa yang paling banyak muncul adalah umur 45. Munculnya sebanyak 5 kali, jadi dapat dijelaskan bahwa kelompok pegawai kantor Y sebagian besar berumur 45 tahun.

• Data Kelompok

RUMUS: Mo = Tb + .C

Keterangan:

• Tb= tepi bawah kelas modus
• a= selisih frekuensi klas modus dengan frekuensi kelas sebelumnya
• b= selisih frekuensi klas modus dengan frekuensi kelas sesudahnya
• c= panjang interval kelas